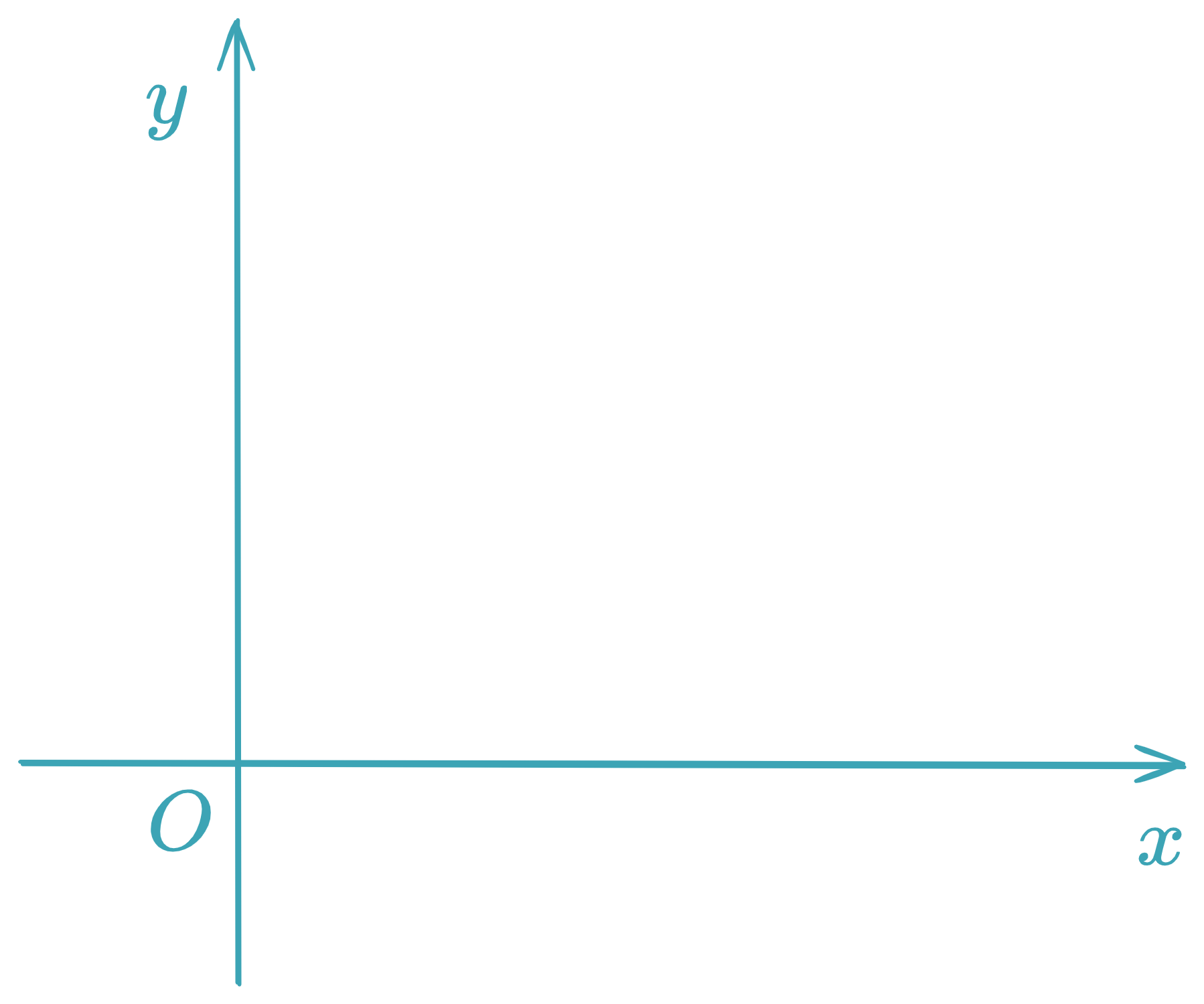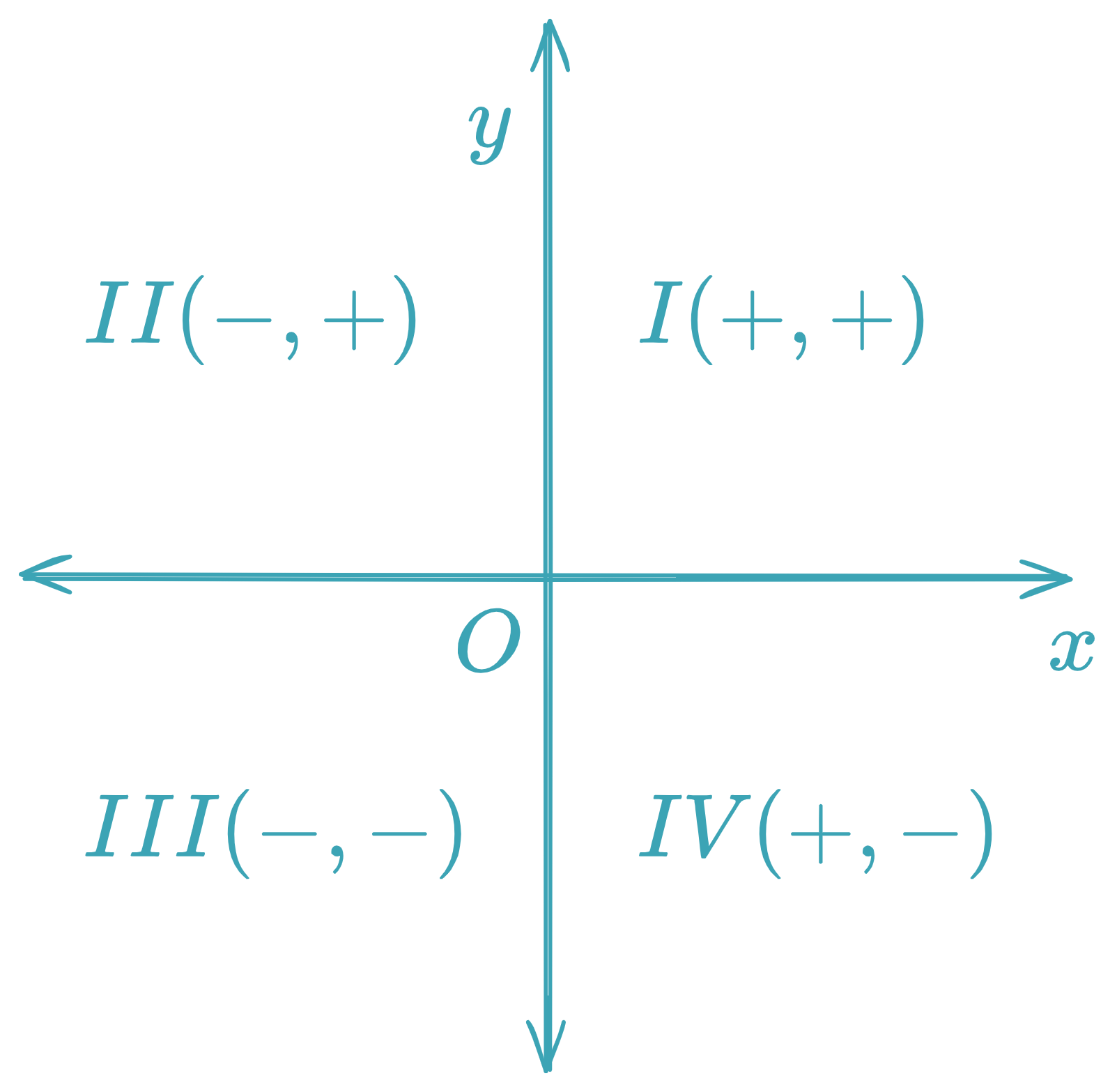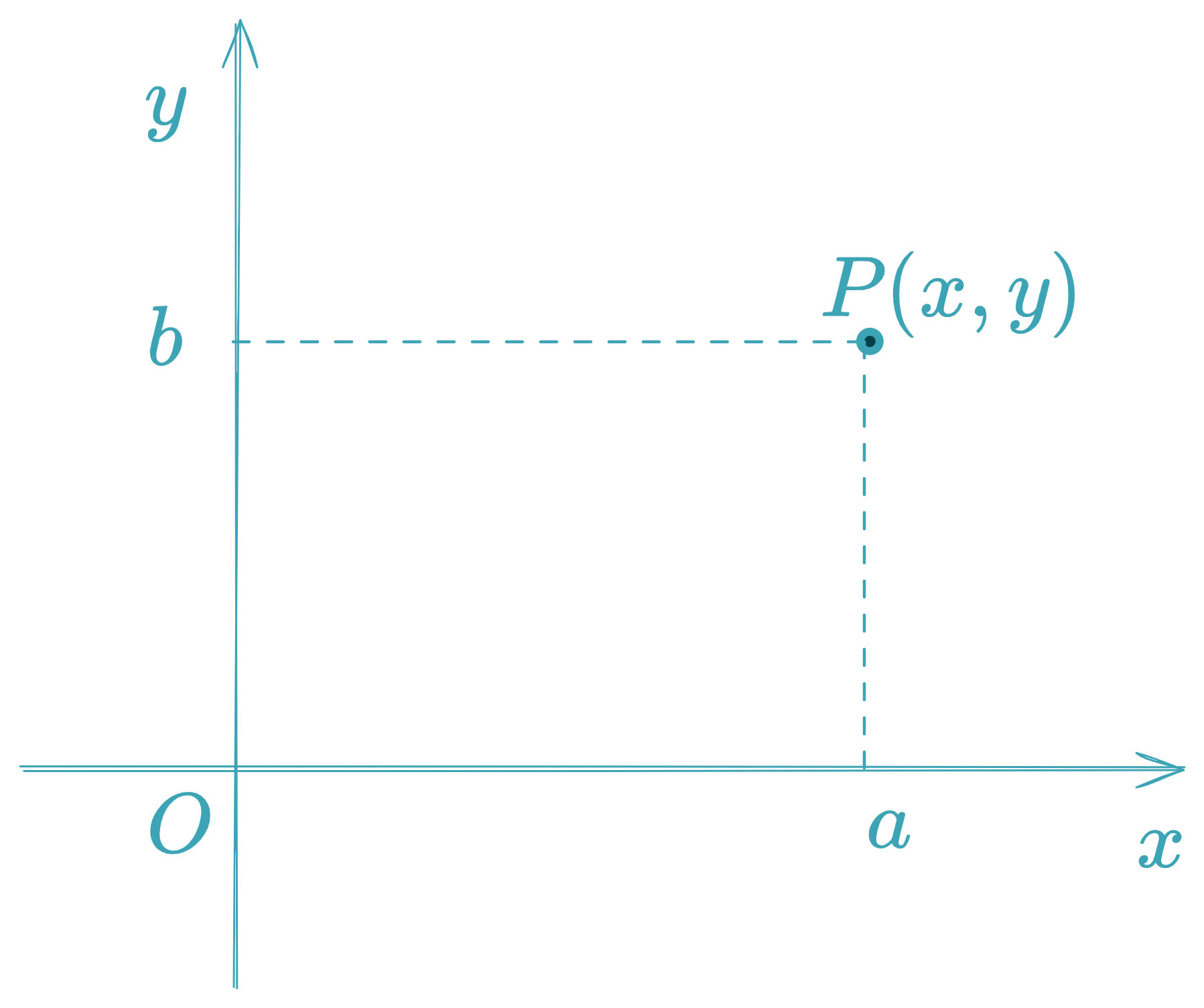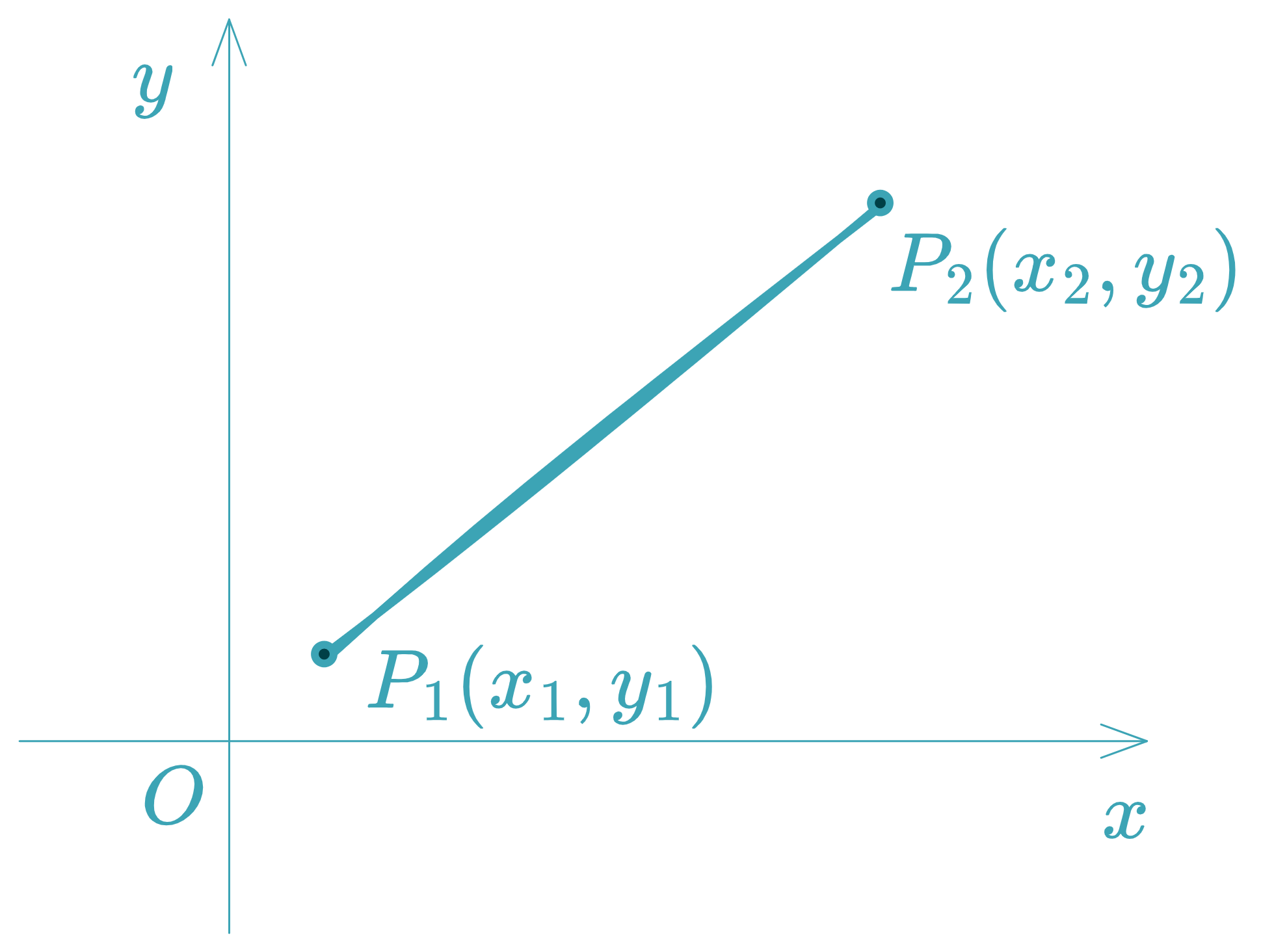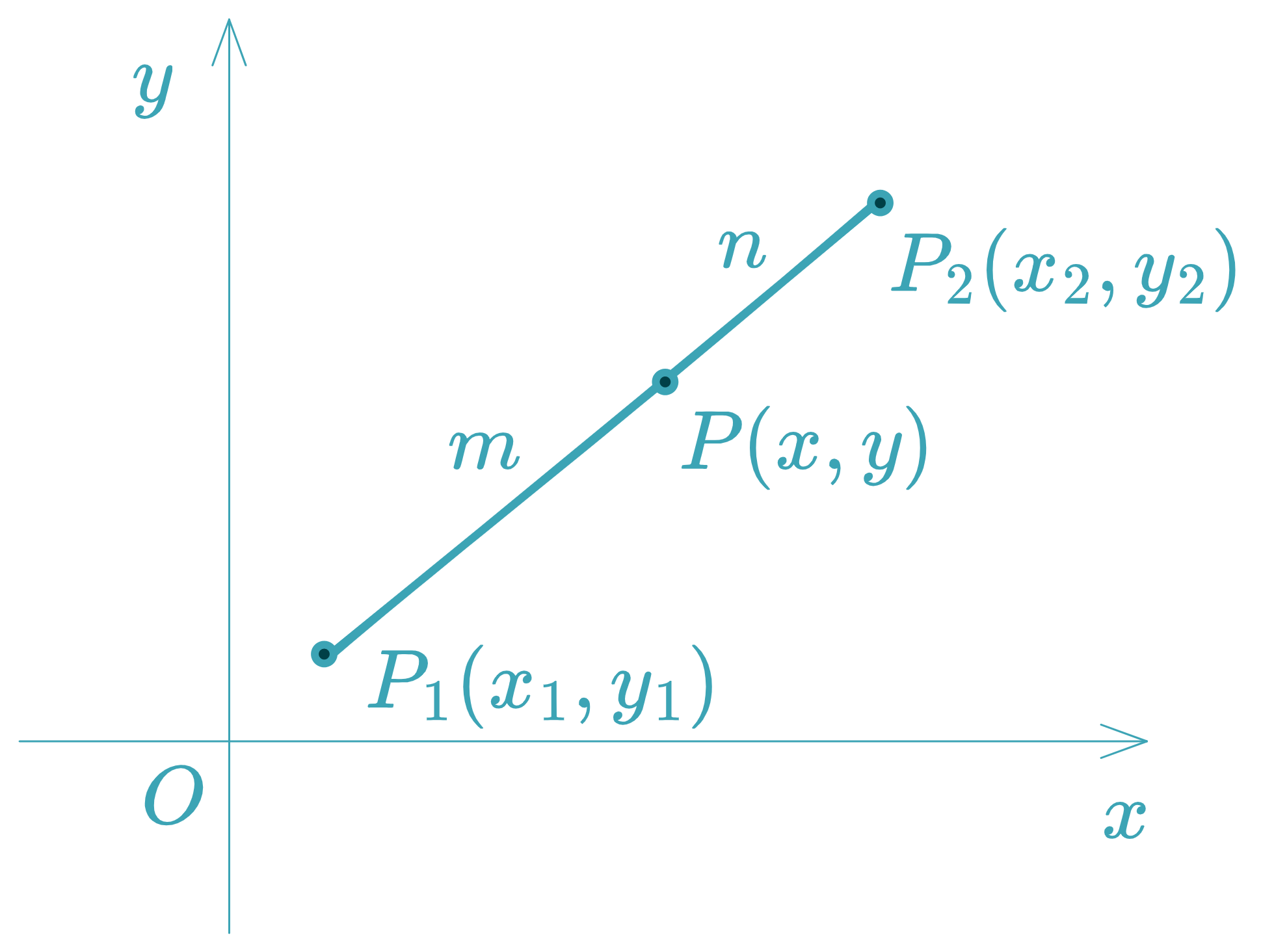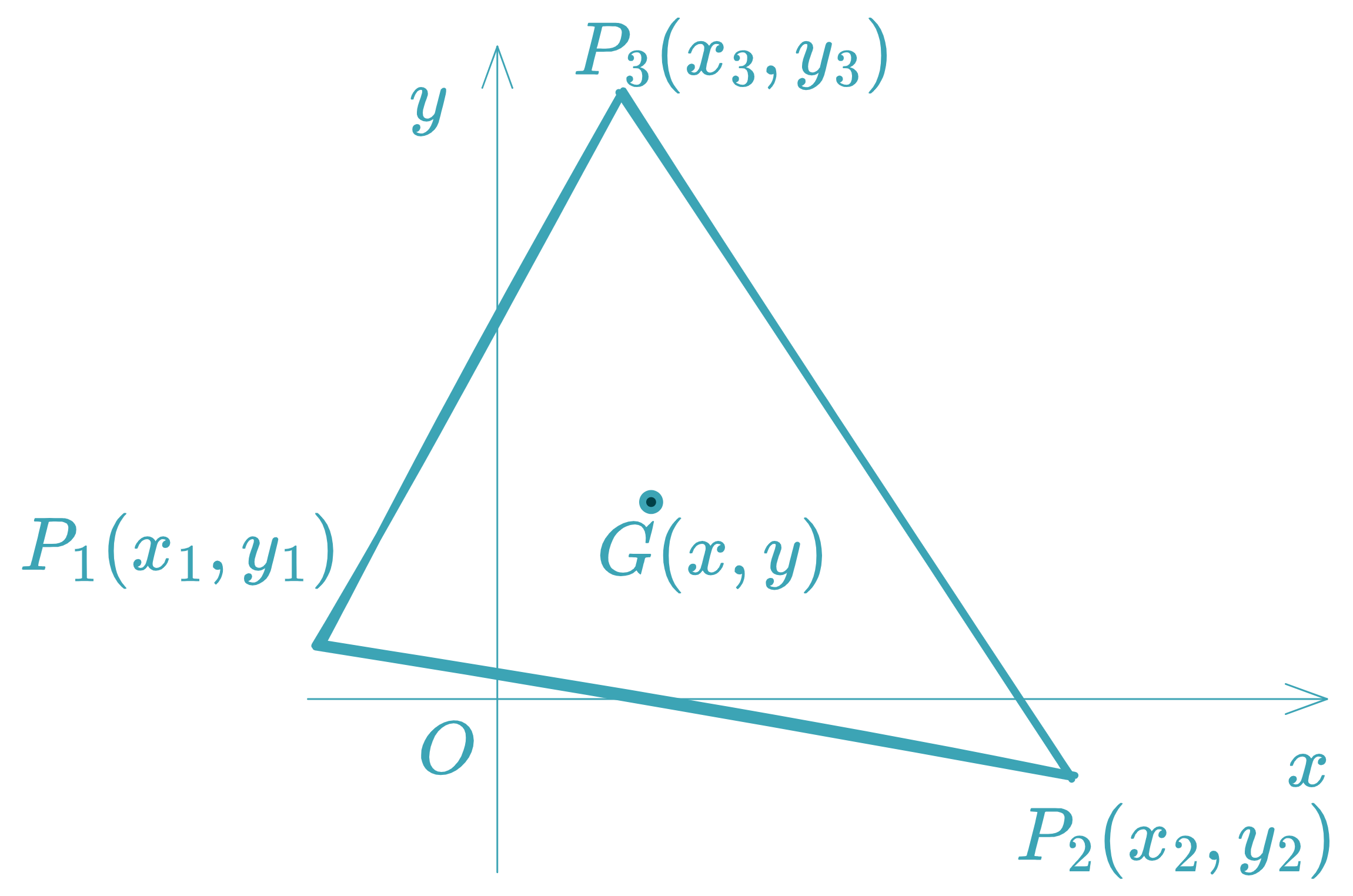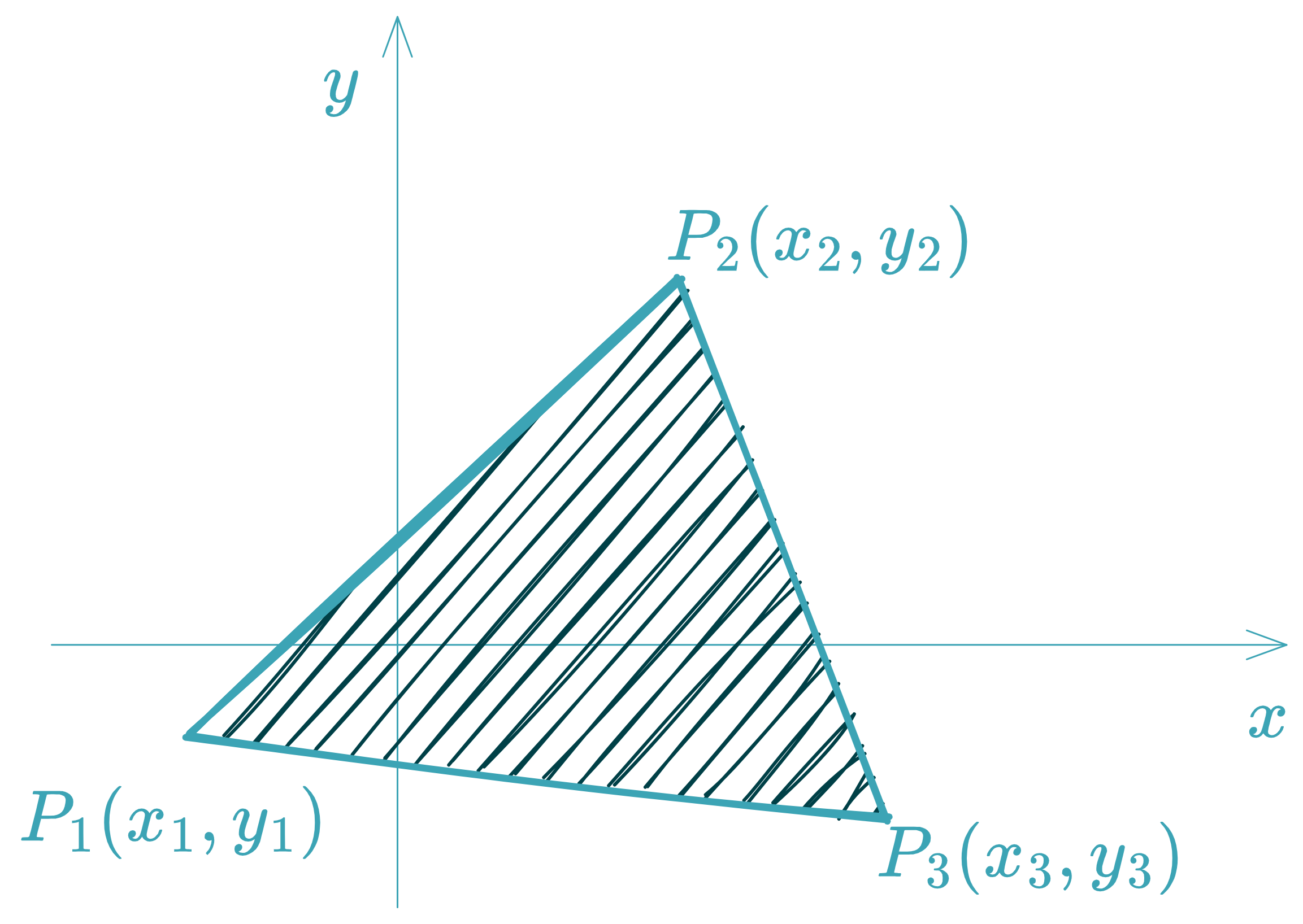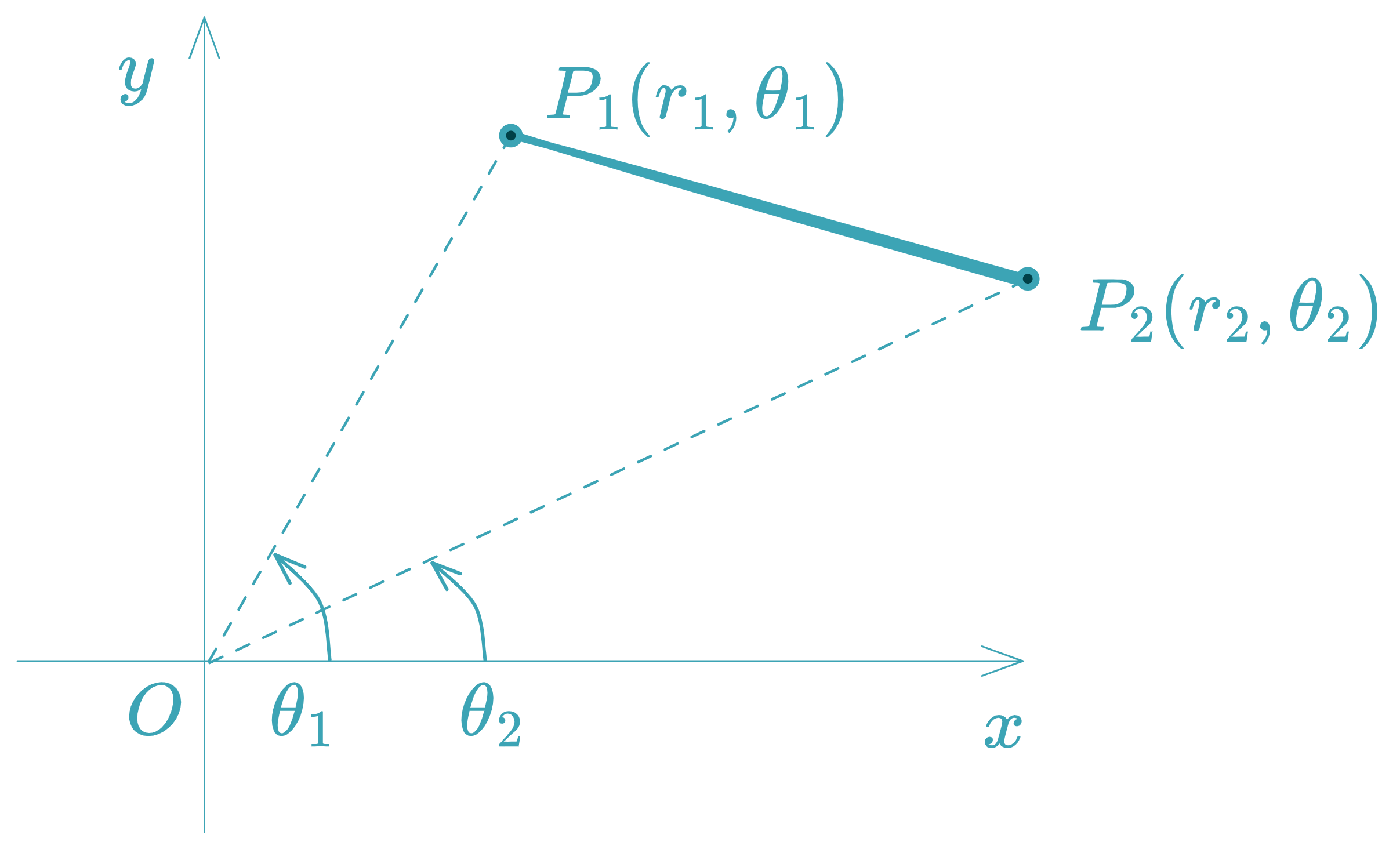Comprehensive summary of fundamental concepts in analytic geometry, including the Cartesian plane, quadrants, point representation, distance calculations (in rectangular and polar coordinates), midpoint, segment division, centroid of a triangle, and formulas for the areas of triangles and polygons. Includes illustrative images and key mathematical formulas.
Table of Contents Cartesian Plane
Rectangular coordinate system : x x x y y y Origin : point ( 0 , 0 ) (0,0) ( 0 , 0 )
Quadrants
Four quadrants numbered I to IV counterclockwiseSigns :
Quadrant I: ( + , + ) (+,+) ( + , + )
Quadrant II: ( − , + ) (-,+) ( − , + )
Quadrant III: ( − , − ) (-,-) ( − , − )
Quadrant IV: ( + , − ) (+,-) ( + , − )
Points
Representation : P ( x , y ) P(x,y) P ( x , y ) Special points :
Origin: O ( 0 , 0 ) O(0,0) O ( 0 , 0 )
On the x x x ( a , 0 ) (a,0) ( a , 0 )
On the y y y ( 0 , b ) (0,b) ( 0 , b )
Distance Between Two Points
For P 1 ( x 1 , y 1 ) P_1(x_1,y_1) P 1 ( x 1 , y 1 ) P 2 ( x 2 , y 2 ) P_2(x_2,y_2) P 2 ( x 2 , y 2 )
d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}
d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2
Distance Between Two Points in Polar Coordinates
Given two points in polar coordinates:
P 1 ( r 1 , θ 1 ) P_1(r_1, \theta_1) P 1 ( r 1 , θ 1 ) P 2 ( r 2 , θ 2 ) P_2(r_2, \theta_2) P 2 ( r 2 , θ 2 )
The distance d d d
d = r 1 2 + r 2 2 − 2 r 1 r 2 cos ( θ 2 − θ 1 ) d = \sqrt{r_1^2 + r_2^2 - 2r_1r_2 \cos(\theta_2 - \theta_1)}
d = r 1 2 + r 2 2 − 2 r 1 r 2 cos ( θ 2 − θ 1 )
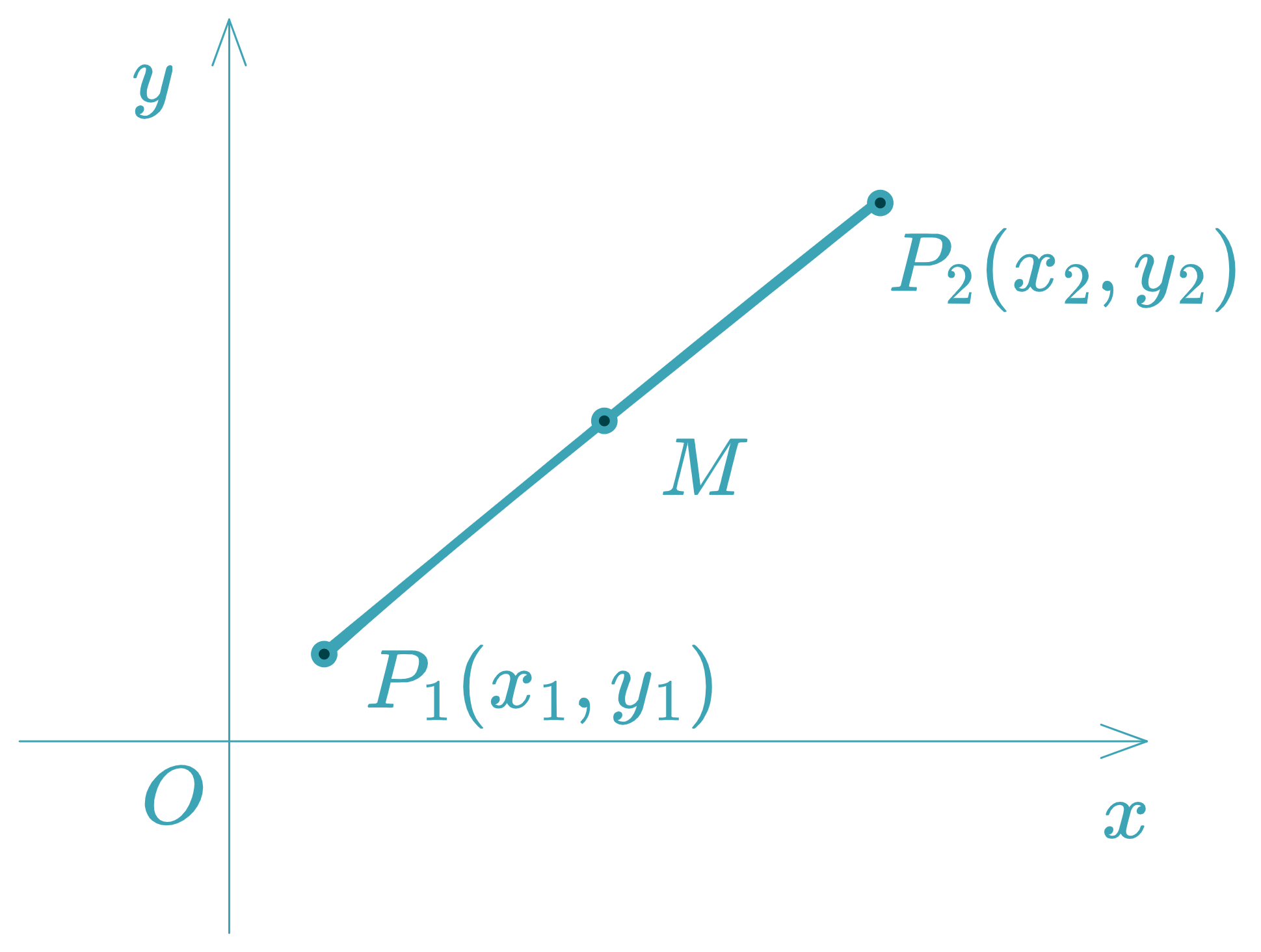
Midpoint
Midpoint M M M P 1 ( x 1 , y 1 ) P_1(x_1,y_1) P 1 ( x 1 , y 1 ) P 2 ( x 2 , y 2 ) P_2(x_2,y_2) P 2 ( x 2 , y 2 )
M ( x 1 + x 2 2 , y 1 + y 2 2 ) M\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)
M ( 2 x 1 + x 2 , 2 y 1 + y 2 )
Division of a Segment in a Given Ratio
Point P P P P 1 P 2 P_1P_2 P 1 P 2 P 1 P P P 2 = m n = λ \frac{P_1P}{PP_2}=\frac{m}{n}=\lambda P P 2 P 1 P = n m = λ
x = n x 1 + m x 2 n + m = x 1 + λ x 2 1 + λ , y = n y 1 + m y 2 n + m = y 1 + λ y 2 1 + λ x=\frac{nx_1+mx_2}{n+m}=\frac{x_1+\lambda x_2}{1+\lambda},\quad y=\frac{ny_1+my_2}{n+m}=\frac{y_1+\lambda y_2}{1+\lambda}
x = n + m n x 1 + m x 2 = 1 + λ x 1 + λ x 2 , y = n + m n y 1 + m y 2 = 1 + λ y 1 + λ y 2
P ( x 1 + λ x 2 1 + λ , y 1 + λ y 2 1 + λ ) P\left(\frac{x_1+\lambda x_2}{1+\lambda }, \frac{y_1+\lambda y_2}{1+\lambda }\right)
P ( 1 + λ x 1 + λ x 2 , 1 + λ y 1 + λ y 2 )
Coordinates of the Centroid of a Triangle
x = x 1 + x 2 + x 3 3 x=\frac{x_1+x_2+x_3}{3}
x = 3 x 1 + x 2 + x 3
y = y 1 + y 2 + y 3 3 y=\frac{y_1+y_2+y_3}{3}
y = 3 y 1 + y 2 + y 3
Area of a Triangle
Given the vertices ( x 1 , y 1 ) (x_1, y_1) ( x 1 , y 1 ) ( x 2 , y 2 ) (x_2, y_2) ( x 2 , y 2 ) ( x 3 , y 3 ) (x_3, y_3) ( x 3 , y 3 )
Area = 1 2 ∣ ∣ x 1 y 1 1 x 2 y 2 1 x 3 y 3 1 ∣ ∣ \text{Area} = \frac{1}{2} \left|
\begin{vmatrix}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1 \\
\end{vmatrix}
\right|
Area = 2 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ x 1 x 2 x 3 y 1 y 2 y 3 1 1 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣
Where the determinant is calculated as:
∣ x 1 y 1 1 x 2 y 2 1 x 3 y 3 1 ∣ = x 1 ( y 2 − y 3 ) − y 1 ( x 2 − x 3 ) + 1 ( x 2 y 3 − x 3 y 2 ) \begin{vmatrix}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1 \\
\end{vmatrix}
= x_1(y_2 - y_3) - y_1(x_2 - x_3) + 1(x_2 y_3 - x_3 y_2)
∣ ∣ ∣ ∣ ∣ ∣ ∣ x 1 x 2 x 3 y 1 y 2 y 3 1 1 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ = x 1 ( y 2 − y 3 ) − y 1 ( x 2 − x 3 ) + 1 ( x 2 y 3 − x 3 y 2 )
In practice, it simplifies to:
Area = 1 2 ∣ x 1 ( y 2 − y 3 ) + x 2 ( y 3 − y 1 ) + x 3 ( y 1 − y 2 ) ∣ \text{Area} = \frac{1}{2} \big| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \big|
Area = 2 1 ∣ ∣ ∣ x 1 ( y 2 − y 3 ) + x 2 ( y 3 − y 1 ) + x 3 ( y 1 − y 2 ) ∣ ∣ ∣
Example
Given vertices P 1 ( 2 , 4 ) P_1(2, 4) P 1 ( 2 , 4 ) P 2 ( 5 , 6 ) P_2(5, 6) P 2 ( 5 , 6 ) P 3 ( 3 , 1 ) P_3(3, 1) P 3 ( 3 , 1 )
Construct the matrix :
∣ 2 4 1 5 6 1 3 1 1 ∣ \begin{vmatrix}
2 & 4 & 1 \\
5 & 6 & 1 \\
3 & 1 & 1 \\
\end{vmatrix} ∣ ∣ ∣ ∣ ∣ ∣ ∣ 2 5 3 4 6 1 1 1 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣
Calculate the determinant (Sarrus' rule):
= 2 ( 6 ⋅ 1 − 1 ⋅ 1 ) − 4 ( 5 ⋅ 1 − 3 ⋅ 1 ) + 1 ( 5 ⋅ 1 − 3 ⋅ 6 ) = 2(6 \cdot 1 - 1 \cdot 1) - 4(5 \cdot 1 - 3 \cdot 1) + 1(5 \cdot 1 - 3 \cdot 6)
= 2 ( 6 ⋅ 1 − 1 ⋅ 1 ) − 4 ( 5 ⋅ 1 − 3 ⋅ 1 ) + 1 ( 5 ⋅ 1 − 3 ⋅ 6 )
= 2 ( 6 − 1 ) − 4 ( 5 − 3 ) + 1 ( 5 − 18 ) = 2(6 - 1) - 4(5 - 3) + 1(5 - 18)
= 2 ( 6 − 1 ) − 4 ( 5 − 3 ) + 1 ( 5 − 1 8 )
= 2 ( 5 ) − 4 ( 2 ) + 1 ( − 13 ) = 10 − 8 − 13 = − 11 = 2(5) - 4(2) + 1(-13) = 10 - 8 - 13 = -11
= 2 ( 5 ) − 4 ( 2 ) + 1 ( − 1 3 ) = 1 0 − 8 − 1 3 = − 1 1
Take the absolute value and divide by 2 :
Area = 1 2 ∣ − 11 ∣ = 5.5 u 2 \text{Area} = \frac{1}{2} |-11| = 5.5 \text{ u}^2
Area = 2 1 ∣ − 1 1 ∣ = 5 . 5 u 2
Area of a Polygon
For vertices ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) (x_1,y_1), (x_2,y_2), \ldots, (x_n,y_n) ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n )
Area = 1 2 ∣ ∑ i = 1 n ( x i y i + 1 ) − ∑ i = 1 n ( y i x i + 1 ) ∣ \text{Area} = \frac{1}{2} \left| \sum_{i=1}^{n} \left( x_i y_{i+1} \right) - \sum_{i=1}^{n} \left( y_i x_{i+1} \right) \right|
Area = 2 1 ∣ ∣ ∣ ∣ ∣ ∣ i = 1 ∑ n ( x i y i + 1 ) − i = 1 ∑ n ( y i x i + 1 ) ∣ ∣ ∣ ∣ ∣ ∣
where:
x n + 1 = x 1 x_{n+1} = x_1 x n + 1 = x 1 y n + 1 = y 1 y_{n+1} = y_1 y n + 1 = y 1 Vertices must be ordered clockwise or counterclockwise (no crossings).
Ordered list of vertices : Write the coordinates in order (e.g., P 1 → P 2 → P 3 → ⋯ → P 1 P_1 \to P_2 \to P_3 \to \dots \to P_1 P 1 → P 2 → P 3 → ⋯ → P 1 Sum 1 (Σ 1 \Sigma_1 Σ 1 : Multiply each x i x_i x i y y y y i + 1 y_{i+1} y i + 1 Sum 2 (Σ 2 \Sigma_2 Σ 2 : Multiply each y i y_i y i x x x x i + 1 x_{i+1} x i + 1 Subtract and take absolute value : Calculate ∣ Σ 1 − Σ 2 ∣ |\Sigma_1 - \Sigma_2| ∣ Σ 1 − Σ 2 ∣
Example
Vertices in order: P 1 ( 2 , 4 ) P_{1}(2, 4) P 1 ( 2 , 4 ) P 2 ( 5 , 6 ) P_{2}(5, 6) P 2 ( 5 , 6 ) P 3 ( 3 , 1 ) P_{3}(3, 1) P 3 ( 3 , 1 ) P 4 ( 1 , 2 ) P_{4}(1, 2) P 4 ( 1 , 2 )
Close the polygon by repeating P 1 P_{1} P 1 :
( 2 , 4 ) , ( 5 , 6 ) , ( 3 , 1 ) , ( 1 , 2 ) , ( 2 , 4 ) (2,4), (5,6), (3,1), (1,2), (2,4)
( 2 , 4 ) , ( 5 , 6 ) , ( 3 , 1 ) , ( 1 , 2 ) , ( 2 , 4 )
Calculate Σ 1 \Sigma_1 Σ 1 :( 2 × 6 ) + ( 5 × 1 ) + ( 3 × 2 ) + ( 1 × 4 ) = 12 + 5 + 6 + 4 = 27 (2 \times 6) + (5 \times 1) + (3 \times 2) + (1 \times 4) = 12 + 5 + 6 + 4 = 27 ( 2 × 6 ) + ( 5 × 1 ) + ( 3 × 2 ) + ( 1 × 4 ) = 1 2 + 5 + 6 + 4 = 2 7
Calculate Σ 2 \Sigma_2 Σ 2 :( 4 × 5 ) + ( 6 × 3 ) + ( 1 × 1 ) + ( 2 × 2 ) = 20 + 18 + 1 + 4 = 43 (4 \times 5) + (6 \times 3) + (1 \times 1) + (2 \times 2) = 20 + 18 + 1 + 4 = 43 ( 4 × 5 ) + ( 6 × 3 ) + ( 1 × 1 ) + ( 2 × 2 ) = 2 0 + 1 8 + 1 + 4 = 4 3
Area :
Area = 1 2 ∣ 27 − 43 ∣ = 16 2 = 8 u 2 \text{Area} = \frac{1}{2} |27 - 43| = \frac{16}{2} = 8 \text{ u}^2
Area = 2 1 ∣ 2 7 − 4 3 ∣ = 2 1 6 = 8 u 2