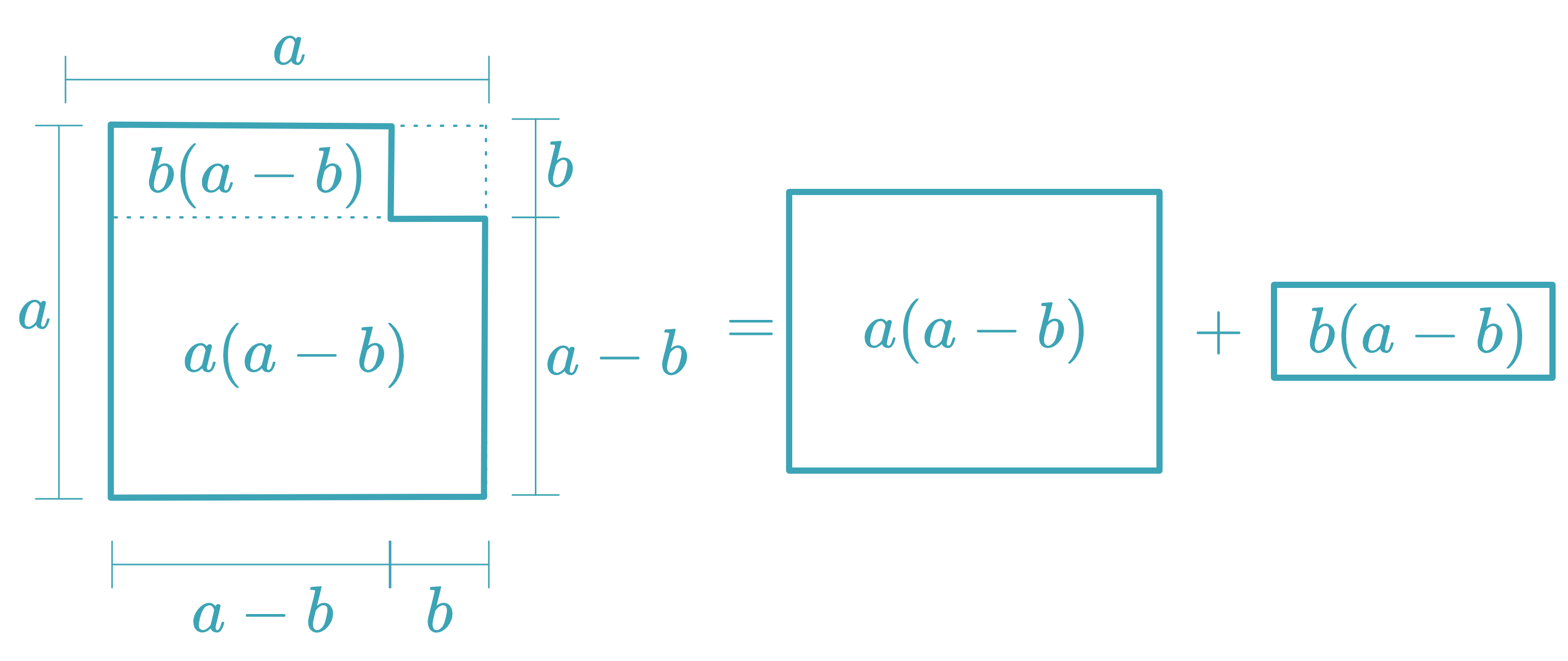Notable Products are multiplications of frequently occurring algebraic expressions whose results can be obtained directly by applying established formulas, without having to perform the operation term by term. These formulas speed up algebraic calculations and are essential tools for simplifying expressions, solving equations, and factoring.
Table of Contents Perfect Square Trinomial
( a + b ) 2 = a 2 + 2 a b + b 2 \boxed{(a + b)^2 = a^2 + 2ab + b^2}
( a + b ) 2 = a 2 + 2 a b + b 2
( a − b ) 2 = a 2 − 2 a b + b 2 \boxed{(a - b)^2 = a^2 - 2ab + b^2}
( a − b ) 2 = a 2 − 2 a b + b 2
( a − b ) 2 = ( b − a ) 2 (a - b)^2 = (b - a)^2
( a − b ) 2 = ( b − a ) 2
Examples
( x + 3 ) 2 = x 2 + 2 ( x ) ( 3 ) + 3 2 = x 2 + 6 x + 9 (x + 3)^2 = x^2 + 2(x)(3) + 3^2 = x^2 + 6x + 9 ( x + 3 ) 2 = x 2 + 2 ( x ) ( 3 ) + 3 2 = x 2 + 6 x + 9 ( 2 a − 5 ) 2 = ( 2 a ) 2 − 2 ( 2 a ) ( 5 ) + 5 2 = 4 a 2 − 20 a + 25 (2a - 5)^2 = (2a)^2 - 2(2a)(5) + 5^2 = 4a^2 - 20a + 25 ( 2 a − 5 ) 2 = ( 2 a ) 2 − 2 ( 2 a ) ( 5 ) + 5 2 = 4 a 2 − 2 0 a + 2 5 ( y + 1 ) 2 = y 2 + 2 ( y ) ( 1 ) + 1 2 = y 2 + 2 y + 1 (y + 1)^2 = y^2 + 2(y)(1) + 1^2 = y^2 + 2y + 1 ( y + 1 ) 2 = y 2 + 2 ( y ) ( 1 ) + 1 2 = y 2 + 2 y + 1 ( 3 x − 2 y ) 2 = ( 3 x ) 2 − 2 ( 3 x ) ( 2 y ) + ( 2 y ) 2 = 9 x 2 − 12 x y + 4 y 2 (3x - 2y)^2 = (3x)^2 - 2(3x)(2y) + (2y)^2 = 9x^2 - 12xy + 4y^2 ( 3 x − 2 y ) 2 = ( 3 x ) 2 − 2 ( 3 x ) ( 2 y ) + ( 2 y ) 2 = 9 x 2 − 1 2 x y + 4 y 2 ( a + 1 2 ) 2 = a 2 + 2 ( a ) ( 1 2 ) + ( 1 2 ) 2 = a 2 + a + 1 4 \left(a + \frac{1}{2}\right)^2 = a^2 + 2(a)\left(\frac{1}{2}\right) + \left(\frac{1}{2}\right)^2 = a^2 + a + \frac{1}{4} ( a + 2 1 ) 2 = a 2 + 2 ( a ) ( 2 1 ) + ( 2 1 ) 2 = a 2 + a + 4 1 ( 5 − b ) 2 = 5 2 − 2 ( 5 ) ( b ) + b 2 = 25 − 10 b + b 2 (5 - b)^2 = 5^2 - 2(5)(b) + b^2 = 25 - 10b + b^2 ( 5 − b ) 2 = 5 2 − 2 ( 5 ) ( b ) + b 2 = 2 5 − 1 0 b + b 2
( a + b ) 2 + ( a − b ) 2 = 2 ( a 2 + b 2 ) (a+b)^2 + (a-b)^2 = 2(a^2 + b^2)
( a + b ) 2 + ( a − b ) 2 = 2 ( a 2 + b 2 )
( a + b ) 2 − ( a − b ) 2 = 4 a b (a + b)^2 - (a - b)^2 = 4ab
( a + b ) 2 − ( a − b ) 2 = 4 a b
( a + b ) 4 − ( a − b ) 4 = 8 a b ( a 2 + b 2 ) (a + b)^4 - (a - b)^4 = 8ab(a^2 + b^2)
( a + b ) 4 − ( a − b ) 4 = 8 a b ( a 2 + b 2 )
Difference of Squares
a 2 − b 2 = ( a + b ) ( a − b ) \boxed{a^2 - b^2 = (a + b)(a - b)}
a 2 − b 2 = ( a + b ) ( a − b )
Examples
x 2 − 9 = x 2 − 3 2 = ( x + 3 ) ( x − 3 ) x^2 - 9 = x^2 - 3^2 = (x + 3)(x - 3) x 2 − 9 = x 2 − 3 2 = ( x + 3 ) ( x − 3 ) 4 a 2 − 25 = ( 2 a ) 2 − 5 2 = ( 2 a + 5 ) ( 2 a − 5 ) 4a^2 - 25 = (2a)^2 - 5^2 = (2a + 5)(2a - 5) 4 a 2 − 2 5 = ( 2 a ) 2 − 5 2 = ( 2 a + 5 ) ( 2 a − 5 ) 16 y 2 − 1 = ( 4 y ) 2 − 1 2 = ( 4 y + 1 ) ( 4 y − 1 ) 16y^2 - 1 = (4y)^2 - 1^2 = (4y + 1)(4y - 1) 1 6 y 2 − 1 = ( 4 y ) 2 − 1 2 = ( 4 y + 1 ) ( 4 y − 1 ) 49 − z 2 = 7 2 − z 2 = ( 7 + z ) ( 7 − z ) 49 - z^2 = 7^2 - z^2 = (7 + z)(7 - z) 4 9 − z 2 = 7 2 − z 2 = ( 7 + z ) ( 7 − z ) x 2 4 − y 2 9 = ( x 2 ) 2 − ( y 3 ) 2 = ( x 2 + y 3 ) ( x 2 − y 3 ) \frac{x^2}{4} - \frac{y^2}{9} = \left(\frac{x}{2}\right)^2 - \left(\frac{y}{3}\right)^2 = \left(\frac{x}{2} + \frac{y}{3}\right)\left(\frac{x}{2} - \frac{y}{3}\right) 4 x 2 − 9 y 2 = ( 2 x ) 2 − ( 3 y ) 2 = ( 2 x + 3 y ) ( 2 x − 3 y ) ( x + 2 ) 2 − 16 = ( x + 2 ) 2 − 4 2 = ( x + 2 + 4 ) ( x + 2 − 4 ) = ( x + 6 ) ( x − 2 ) (x + 2)^2 - 16 = (x + 2)^2 - 4^2 = (x + 2 + 4)(x + 2 - 4) = (x + 6)(x - 2) ( x + 2 ) 2 − 1 6 = ( x + 2 ) 2 − 4 2 = ( x + 2 + 4 ) ( x + 2 − 4 ) = ( x + 6 ) ( x − 2 )
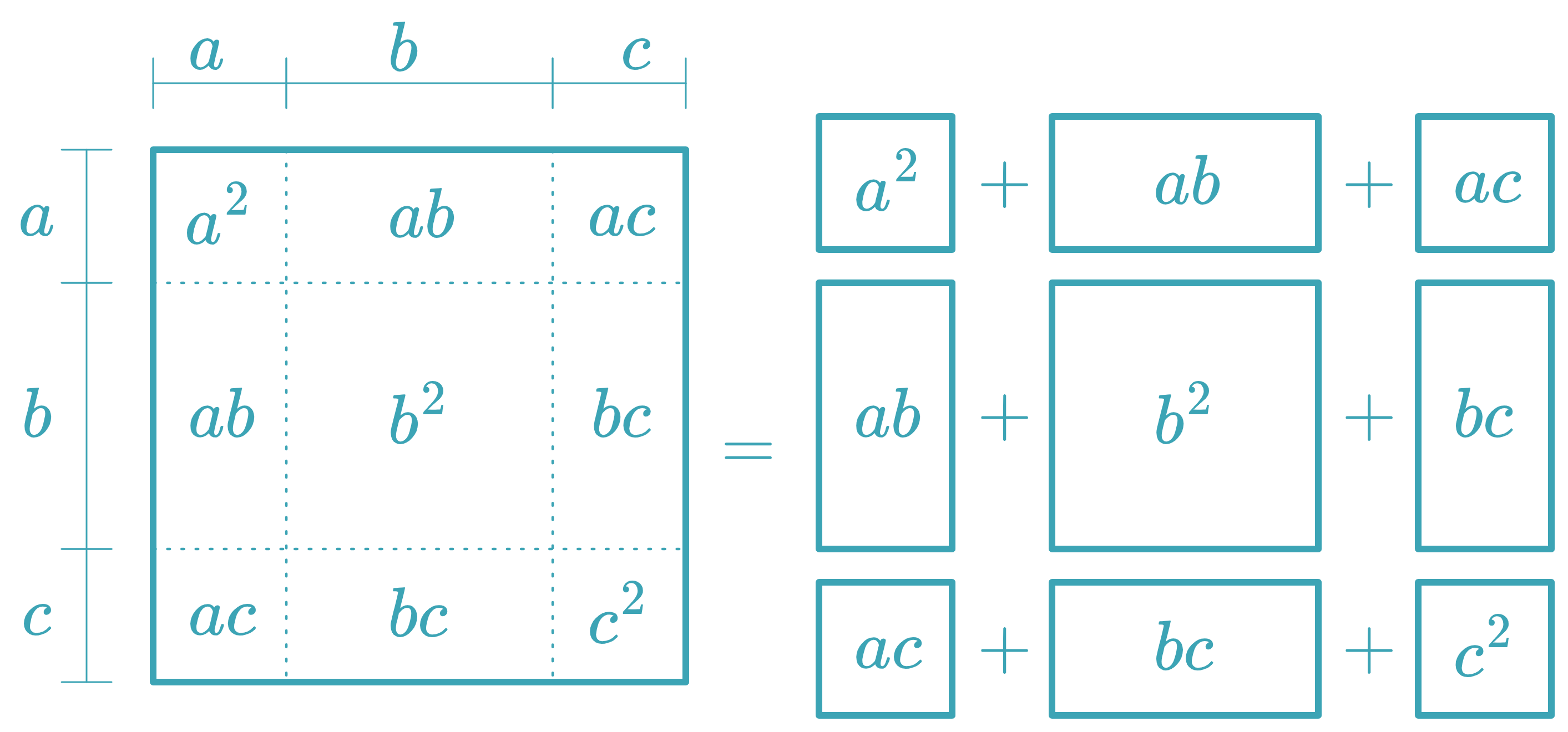
Square of a Trinomial
( a + b + c ) 2 = a 2 + b 2 + c 2 + 2 a b + 2 a c + 2 b c \boxed{(a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2ac + 2bc}
( a + b + c ) 2 = a 2 + b 2 + c 2 + 2 a b + 2 a c + 2 b c
( a + b + c ) 2 = a 2 + b 2 + c 2 + 2 ( a b + a c + b c ) \boxed{(a + b + c)^2 = a^2 + b^2 + c^2 + 2(ab + ac + bc)}
( a + b + c ) 2 = a 2 + b 2 + c 2 + 2 ( a b + a c + b c )
Examples
( x + y + 2 ) 2 = x 2 + y 2 + 4 + 2 x y + 4 x + 4 y (x + y + 2)^2 = x^2 + y^2 + 4 + 2xy + 4x + 4y ( x + y + 2 ) 2 = x 2 + y 2 + 4 + 2 x y + 4 x + 4 y ( a + 3 + b ) 2 = a 2 + 9 + b 2 + 6 a + 2 a b + 6 b (a + 3 + b)^2 = a^2 + 9 + b^2 + 6a + 2ab + 6b ( a + 3 + b ) 2 = a 2 + 9 + b 2 + 6 a + 2 a b + 6 b ( 1 + m + n ) 2 = 1 + m 2 + n 2 + 2 m + 2 n + 2 m n (1 + m + n)^2 = 1 + m^2 + n^2 + 2m + 2n + 2mn ( 1 + m + n ) 2 = 1 + m 2 + n 2 + 2 m + 2 n + 2 m n ( 2 a + 3 b + 1 ) 2 = 4 a 2 + 9 b 2 + 1 + 12 a b + 4 a + 6 b (2a + 3b + 1)^2 = 4a^2 + 9b^2 + 1 + 12ab + 4a + 6b ( 2 a + 3 b + 1 ) 2 = 4 a 2 + 9 b 2 + 1 + 1 2 a b + 4 a + 6 b ( x − 1 + y ) 2 = x 2 + 1 + y 2 − 2 x + 2 x y − 2 y (x - 1 + y)^2 = x^2 + 1 + y^2 - 2x + 2xy - 2y ( x − 1 + y ) 2 = x 2 + 1 + y 2 − 2 x + 2 x y − 2 y ( p + q + r ) 2 = p 2 + q 2 + r 2 + 2 p q + 2 p r + 2 q r (p + q + r)^2 = p^2 + q^2 + r^2 + 2pq + 2pr + 2qr ( p + q + r ) 2 = p 2 + q 2 + r 2 + 2 p q + 2 p r + 2 q r
( a − b + c ) 2 = a 2 + b 2 + c 2 − 2 a b + 2 a c − 2 b c (a - b + c)^2 = a^2 + b^2 + c^2 - 2ab + 2ac - 2bc
( a − b + c ) 2 = a 2 + b 2 + c 2 − 2 a b + 2 a c − 2 b c
( a + b − c ) 2 = a 2 + b 2 + c 2 + 2 a b − 2 a c − 2 b c (a + b - c)^2 = a^2 + b^2 + c^2 + 2ab - 2ac - 2bc
( a + b − c ) 2 = a 2 + b 2 + c 2 + 2 a b − 2 a c − 2 b c
( a − b − c ) 2 = a 2 + b 2 + c 2 − 2 a b − 2 a c + 2 b c (a - b - c)^2 = a^2 + b^2 + c^2 - 2ab - 2ac + 2bc
( a − b − c ) 2 = a 2 + b 2 + c 2 − 2 a b − 2 a c + 2 b c
( a − b − c ) 2 = ( − ( b + c − a ) ) 2 = ( b + c − a ) 2 (a - b - c)^2 = \left(-(b + c - a)\right)^2 = (b + c - a)^2
( a − b − c ) 2 = ( − ( b + c − a ) ) 2 = ( b + c − a ) 2
( a b + b c + a c ) 2 = ( a b ) 2 + ( b c ) 2 + ( a c ) 2 + 2 a b c ( a + b + c ) (ab + bc + ac)^2 = (ab)^2 + (bc)^2 + (ac)^2 + 2abc(a + b + c)
( a b + b c + a c ) 2 = ( a b ) 2 + ( b c ) 2 + ( a c ) 2 + 2 a b c ( a + b + c )
Binomial Cubed
( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 \boxed{(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3}
( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
( a − b ) 3 = a 3 − 3 a 2 b + 3 a b 2 − b 3 \boxed{(a - b)^3 = a^3 - 3a^2b + 3ab^2 - b^3}
( a − b ) 3 = a 3 − 3 a 2 b + 3 a b 2 − b 3
Examples
( x + 2 ) 3 = x 3 + 3 x 2 ( 2 ) + 3 x ( 4 ) + 8 = x 3 + 6 x 2 + 12 x + 8 (x + 2)^3 = x^3 + 3x^2(2) + 3x(4) + 8 = x^3 + 6x^2 + 12x + 8 ( x + 2 ) 3 = x 3 + 3 x 2 ( 2 ) + 3 x ( 4 ) + 8 = x 3 + 6 x 2 + 1 2 x + 8 ( a − 1 ) 3 = a 3 − 3 a 2 ( 1 ) + 3 a ( 1 ) − 1 = a 3 − 3 a 2 + 3 a − 1 (a - 1)^3 = a^3 - 3a^2(1) + 3a(1) - 1 = a^3 - 3a^2 + 3a - 1 ( a − 1 ) 3 = a 3 − 3 a 2 ( 1 ) + 3 a ( 1 ) − 1 = a 3 − 3 a 2 + 3 a − 1 ( 2 x + y ) 3 = ( 2 x ) 3 + 3 ( 4 x 2 ) ( y ) + 3 ( 2 x ) ( y 2 ) + y 3 = 8 x 3 + 12 x 2 y + 6 x y 2 + y 3 (2x + y)^3 = (2x)^3 + 3(4x^2)(y) + 3(2x)(y^2) + y^3 = 8x^3 + 12x^2y + 6xy^2 + y^3 ( 2 x + y ) 3 = ( 2 x ) 3 + 3 ( 4 x 2 ) ( y ) + 3 ( 2 x ) ( y 2 ) + y 3 = 8 x 3 + 1 2 x 2 y + 6 x y 2 + y 3 ( a − 3 b ) 3 = a 3 − 3 a 2 ( 3 b ) + 3 a ( 9 b 2 ) − 27 b 3 = a 3 − 9 a 2 b + 27 a b 2 − 27 b 3 (a - 3b)^3 = a^3 - 3a^2(3b) + 3a(9b^2) - 27b^3 = a^3 - 9a^2b + 27ab^2 - 27b^3 ( a − 3 b ) 3 = a 3 − 3 a 2 ( 3 b ) + 3 a ( 9 b 2 ) − 2 7 b 3 = a 3 − 9 a 2 b + 2 7 a b 2 − 2 7 b 3 ( 1 + x ) 3 = 1 + 3 x + 3 x 2 + x 3 (1 + x)^3 = 1 + 3x + 3x^2 + x^3 ( 1 + x ) 3 = 1 + 3 x + 3 x 2 + x 3 ( x − y ) 3 = x 3 − 3 x 2 y + 3 x y 2 − y 3 (x - y)^3 = x^3 - 3x^2y + 3xy^2 - y^3 ( x − y ) 3 = x 3 − 3 x 2 y + 3 x y 2 − y 3
Short Form (Cauchy's Identities )
( a + b ) 3 = a 3 + b 3 + 3 a b ( a + b ) (a + b)^3 = a^3 + b^3 + 3ab(a + b)
( a + b ) 3 = a 3 + b 3 + 3 a b ( a + b )
( a − b ) 3 = a 3 − b 3 − 3 a b ( a − b ) (a - b)^3 = a^3 - b^3 - 3ab(a - b)
( a − b ) 3 = a 3 − b 3 − 3 a b ( a − b )
( a + b ) 3 + ( a − b ) 3 = 2 a ( a 2 + 3 b 2 ) (a + b)^3 + (a - b)^3 = 2a(a^2 + 3b^2)
( a + b ) 3 + ( a − b ) 3 = 2 a ( a 2 + 3 b 2 )
( a + b ) 3 − ( a − b ) 3 = 2 b ( 3 a 2 + b 2 ) (a + b)^3 - (a - b)^3 = 2b(3a^2 + b^2)
( a + b ) 3 − ( a − b ) 3 = 2 b ( 3 a 2 + b 2 )
Product of Binomials with a Common Term (Stevin's Identity )
( x + a ) ( x + b ) = x 2 + ( a + b ) x + a b \boxed{(x + a)(x + b) = x^2 + (a + b)x + ab}
( x + a ) ( x + b ) = x 2 + ( a + b ) x + a b
( x − a ) ( x − b ) = x 2 − ( a + b ) x + a b (x - a)(x - b) = x^2 - (a + b)x + ab
( x − a ) ( x − b ) = x 2 − ( a + b ) x + a b
( x + a ) ( x + b ) ( x + c ) = x 3 + ( a + b + c ) x 2 + ( a b + b c + a c ) x + a b c (x + a)(x + b)(x + c) = x^3 + (a + b + c)x^2 + (ab + bc + ac)x + abc
( x + a ) ( x + b ) ( x + c ) = x 3 + ( a + b + c ) x 2 + ( a b + b c + a c ) x + a b c
( x − a ) ( x − b ) ( x − c ) = x 3 − ( a + b + c ) x 2 + ( a b + b c + a c ) x − a b c (x - a)(x - b)(x - c) = x^3 - (a + b + c)x^2 + (ab + bc + ac)x - abc
( x − a ) ( x − b ) ( x − c ) = x 3 − ( a + b + c ) x 2 + ( a b + b c + a c ) x − a b c
Examples
( x + 3 ) ( x + 5 ) = x 2 + ( 3 + 5 ) x + 3 ⋅ 5 = x 2 + 8 x + 15 (x + 3)(x + 5) = x^2 + (3 + 5)x + 3 \cdot 5 = x^2 + 8x + 15 ( x + 3 ) ( x + 5 ) = x 2 + ( 3 + 5 ) x + 3 ⋅ 5 = x 2 + 8 x + 1 5 ( x + 2 ) ( x − 7 ) = x 2 + ( 2 − 7 ) x + 2 ⋅ ( − 7 ) = x 2 − 5 x − 14 (x + 2)(x - 7) = x^2 + (2 - 7)x + 2 \cdot (-7) = x^2 - 5x - 14 ( x + 2 ) ( x − 7 ) = x 2 + ( 2 − 7 ) x + 2 ⋅ ( − 7 ) = x 2 − 5 x − 1 4 ( x − 4 ) ( x − 6 ) = x 2 + ( − 4 − 6 ) x + ( − 4 ) ⋅ ( − 6 ) = x 2 − 10 x + 24 (x - 4)(x - 6) = x^2 + (-4 - 6)x + (-4) \cdot (-6) = x^2 - 10x + 24 ( x − 4 ) ( x − 6 ) = x 2 + ( − 4 − 6 ) x + ( − 4 ) ⋅ ( − 6 ) = x 2 − 1 0 x + 2 4 ( x + 1 ) ( x + 9 ) = x 2 + ( 1 + 9 ) x + 1 ⋅ 9 = x 2 + 10 x + 9 (x + 1)(x + 9) = x^2 + (1 + 9)x + 1 \cdot 9 = x^2 + 10x + 9 ( x + 1 ) ( x + 9 ) = x 2 + ( 1 + 9 ) x + 1 ⋅ 9 = x 2 + 1 0 x + 9 ( x − 3 ) ( x + 8 ) = x 2 + ( − 3 + 8 ) x + ( − 3 ) ⋅ 8 = x 2 + 5 x − 24 (x - 3)(x + 8) = x^2 + (-3 + 8)x + (-3) \cdot 8 = x^2 + 5x - 24 ( x − 3 ) ( x + 8 ) = x 2 + ( − 3 + 8 ) x + ( − 3 ) ⋅ 8 = x 2 + 5 x − 2 4 ( x + a ) ( x + b ) = x 2 + ( a + b ) x + a b (x + a)(x + b) = x^2 + (a + b)x + ab ( x + a ) ( x + b ) = x 2 + ( a + b ) x + a b
Trinomial Cubed
( a + b + c ) 3 = a 3 + b 3 + c 3 + 3 ( a + b ) ( b + c ) ( c + a ) \boxed{(a + b + c)^3 = a^3 + b^3 + c^3 + 3(a + b)(b + c)(c + a)}
( a + b + c ) 3 = a 3 + b 3 + c 3 + 3 ( a + b ) ( b + c ) ( c + a )
( a + b + c ) 3 = a 3 + b 3 + c 3 + 3 ( a + b ) ( b + c ) ( c + a ) − 3 a b c (a + b + c)^3 = a^3 + b^3 + c^3 + 3(a + b)(b + c)(c + a) - 3abc
( a + b + c ) 3 = a 3 + b 3 + c 3 + 3 ( a + b ) ( b + c ) ( c + a ) − 3 a b c
( a + b + c ) 3 = 3 ( a + b + c ) ( a 2 + b 2 + c 2 ) − 2 ( a 3 + b 3 + c 3 ) + 6 a b c (a + b + c)^3 = 3(a + b + c)(a^2 + b^2 + c^2) - 2(a^3 + b^3 + c^3) + 6abc
( a + b + c ) 3 = 3 ( a + b + c ) ( a 2 + b 2 + c 2 ) − 2 ( a 3 + b 3 + c 3 ) + 6 a b c
( a + b + c ) 3 = a 3 + b 3 + c 3 + 3 a 2 ( b + c ) + 3 b 2 ( a + c ) + 3 c 2 ( a + b ) + 6 a b c (a + b + c)^3 = a^3 + b^3 + c^3 + 3a^2(b + c) + 3b^2(a + c) + 3c^2(a + b) + 6abc
( a + b + c ) 3 = a 3 + b 3 + c 3 + 3 a 2 ( b + c ) + 3 b 2 ( a + c ) + 3 c 2 ( a + b ) + 6 a b c
Examples
( x + 1 + 2 ) 3 = x 3 + 1 3 + 2 3 + 3 ( x + 1 ) ( 1 + 2 ) ( 2 + x ) = x 3 + 1 + 8 + 9 ( x + 1 ) ( x + 2 ) (x + 1 + 2)^3 = x^3 + 1^3 + 2^3 + 3(x + 1)(1 + 2)(2 + x) = x^3 + 1 + 8 + 9(x + 1)(x + 2) ( x + 1 + 2 ) 3 = x 3 + 1 3 + 2 3 + 3 ( x + 1 ) ( 1 + 2 ) ( 2 + x ) = x 3 + 1 + 8 + 9 ( x + 1 ) ( x + 2 ) ( 1 + 2 + 3 ) 3 = 1 3 + 2 3 + 3 3 + 3 ( 1 + 2 ) ( 2 + 3 ) ( 3 + 1 ) = 1 + 8 + 27 + 180 = 216 (1 + 2 + 3)^3 = 1^3 + 2^3 + 3^3 + 3(1 + 2)(2 + 3)(3 + 1) = 1 + 8 + 27 + 180 = 216 ( 1 + 2 + 3 ) 3 = 1 3 + 2 3 + 3 3 + 3 ( 1 + 2 ) ( 2 + 3 ) ( 3 + 1 ) = 1 + 8 + 2 7 + 1 8 0 = 2 1 6 ( a + 0 + b ) 3 = a 3 + b 3 + 3 a b ( a + b ) = a 3 + 3 a 2 b + 3 a b 2 + b 3 (a + 0 + b)^3 = a^3 + b^3 + 3ab(a + b) = a^3 + 3a^2b + 3ab^2 + b^3 ( a + 0 + b ) 3 = a 3 + b 3 + 3 a b ( a + b ) = a 3 + 3 a 2 b + 3 a b 2 + b 3 ( x + y + 0 ) 3 = x 3 + y 3 + 3 x y ( x + y ) (x + y + 0)^3 = x^3 + y^3 + 3xy(x + y) ( x + y + 0 ) 3 = x 3 + y 3 + 3 x y ( x + y ) ( 1 + x + 1 ) 3 = ( x + 2 ) 3 = x 3 + 8 + 6 ( x + 1 ) 2 (1 + x + 1)^3 = (x + 2)^3 = x^3 + 8 + 6(x + 1)^2 ( 1 + x + 1 ) 3 = ( x + 2 ) 3 = x 3 + 8 + 6 ( x + 1 ) 2 ( a + b + c ) 3 = a 3 + b 3 + c 3 + 3 ( a + b ) ( b + c ) ( c + a ) (a + b + c)^3 = a^3 + b^3 + c^3 + 3(a + b)(b + c)(c + a) ( a + b + c ) 3 = a 3 + b 3 + c 3 + 3 ( a + b ) ( b + c ) ( c + a )
Sum and Difference of Cubes
a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 ) \boxed{a^3 + b^3 = (a + b)(a^2 - ab + b^2)}
a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 )
a 3 − b 3 = ( a − b ) ( a 2 + a b + b 2 ) \boxed{a^3 - b^3 = (a - b)(a^2 + ab + b^2)}
a 3 − b 3 = ( a − b ) ( a 2 + a b + b 2 )
Examples
8 + 27 = 2 3 + 3 3 = ( 2 + 3 ) ( 4 − 6 + 9 ) = 5 ⋅ 7 = 35 8 + 27 = 2^3 + 3^3 = (2 + 3)(4 - 6 + 9) = 5 \cdot 7 = 35 8 + 2 7 = 2 3 + 3 3 = ( 2 + 3 ) ( 4 − 6 + 9 ) = 5 ⋅ 7 = 3 5 x 3 − 8 = x 3 − 2 3 = ( x − 2 ) ( x 2 + 2 x + 4 ) x^3 - 8 = x^3 - 2^3 = (x - 2)(x^2 + 2x + 4) x 3 − 8 = x 3 − 2 3 = ( x − 2 ) ( x 2 + 2 x + 4 ) 64 + 125 = 4 3 + 5 3 = ( 4 + 5 ) ( 16 − 20 + 25 ) = 9 ⋅ 21 = 189 64 + 125 = 4^3 + 5^3 = (4 + 5)(16 - 20 + 25) = 9 \cdot 21 = 189 6 4 + 1 2 5 = 4 3 + 5 3 = ( 4 + 5 ) ( 1 6 − 2 0 + 2 5 ) = 9 ⋅ 2 1 = 1 8 9 27 a 3 − 64 b 3 = ( 3 a ) 3 − ( 4 b ) 3 = ( 3 a − 4 b ) ( 9 a 2 + 12 a b + 16 b 2 ) 27a^3 - 64b^3 = (3a)^3 - (4b)^3 = (3a - 4b)(9a^2 + 12ab + 16b^2) 2 7 a 3 − 6 4 b 3 = ( 3 a ) 3 − ( 4 b ) 3 = ( 3 a − 4 b ) ( 9 a 2 + 1 2 a b + 1 6 b 2 ) 1 + x 3 = ( 1 + x ) ( 1 − x + x 2 ) 1 + x^3 = (1 + x)(1 - x + x^2) 1 + x 3 = ( 1 + x ) ( 1 − x + x 2 ) y 3 + 1000 = ( y + 10 ) ( y 2 − 10 y + 100 ) y^3 + 1000 = (y + 10)(y^2 - 10y + 100) y 3 + 1 0 0 0 = ( y + 1 0 ) ( y 2 − 1 0 y + 1 0 0 )
Argand's Identities
( a 2 + a + 1 ) ( a 2 − a + 1 ) = a 4 + a 2 + 1 \boxed{(a^2 + a + 1)(a^2 - a + 1) = a^4 + a^2 + 1}
( a 2 + a + 1 ) ( a 2 − a + 1 ) = a 4 + a 2 + 1
( a 2 + a b + b 2 ) ( a 2 − a b + b 2 ) = a 4 + a 2 b 2 + b 4 \boxed{(a^2 + ab + b^2)(a^2 - ab + b^2) = a^4 + a^2b^2 + b^4}
( a 2 + a b + b 2 ) ( a 2 − a b + b 2 ) = a 4 + a 2 b 2 + b 4
( a 2 m + a m b n + b 2 n ) ( a 2 m − a m b n + b 2 n ) = a 4 m + a 2 m b 2 n + b 4 n (a^{2m} + a^m b^n + b^{2n})(a^{2m} - a^m b^n + b^{2n}) = a^{4m} + a^{2m}b^{2n} + b^{4n}
( a 2 m + a m b n + b 2 n ) ( a 2 m − a m b n + b 2 n ) = a 4 m + a 2 m b 2 n + b 4 n
Gauss's Identity
a 3 + b 3 + c 3 − 3 a b c = ( a + b + c ) ( a 2 + b 2 + c 2 − a b − a c − b c ) a^3 + b^3 + c^3 - 3abc = (a + b + c)(a^2 + b^2 + c^2 - ab - ac - bc)
a 3 + b 3 + c 3 − 3 a b c = ( a + b + c ) ( a 2 + b 2 + c 2 − a b − a c − b c )
( a + b ) ( b + c ) ( a + c ) + a b c = ( a + b + c ) ( a b + a c + b c ) (a + b)(b + c)(a + c) + abc = (a + b + c)(ab + ac + bc)
( a + b ) ( b + c ) ( a + c ) + a b c = ( a + b + c ) ( a b + a c + b c )
a 2 + b 2 + c 2 − a b − a c − b c = 1 2 [ ( a − b ) 2 + ( a − c ) 2 + ( b − c ) 2 ] a^2 + b^2 + c^2 - ab - ac - bc = \frac{1}{2}\left[(a - b)^2 + (a - c)^2 + (b - c)^2\right]
a 2 + b 2 + c 2 − a b − a c − b c = 2 1 [ ( a − b ) 2 + ( a − c ) 2 + ( b − c ) 2 ]
Lagrange's Identities
( a x + b y ) 2 + ( a y − b x ) 2 = ( a 2 + b 2 ) ( x 2 + y 2 ) (ax + by)^2 + (ay - bx)^2 = (a^2 + b^2)(x^2 + y^2)
( a x + b y ) 2 + ( a y − b x ) 2 = ( a 2 + b 2 ) ( x 2 + y 2 )
( a x + b y + c z ) 2 + ( a y − b x ) 2 + ( b z − c y ) 2 + ( a z − c x ) 2 = ( a 2 + b 2 + c 2 ) ( x 2 + y 2 + z 2 ) (ax + by + cz)^2 + (ay - bx)^2 + (bz - cy)^2 + (az - cx)^2 = (a^2 + b^2 + c^2)(x^2 + y^2 + z^2)
( a x + b y + c z ) 2 + ( a y − b x ) 2 + ( b z − c y ) 2 + ( a z − c x ) 2 = ( a 2 + b 2 + c 2 ) ( x 2 + y 2 + z 2 )
a 2 + b 2 = ( a + b ) 2 − 2 a b a^2 + b^2 = (a + b)^2 - 2ab
a 2 + b 2 = ( a + b ) 2 − 2 a b
a 3 + b 3 = ( a + b ) 3 − 3 a b ( a + b ) a^3 + b^3 = (a + b)^3 - 3ab(a + b)
a 3 + b 3 = ( a + b ) 3 − 3 a b ( a + b )
a 4 + b 4 = ( a + b ) 4 − 4 a b ( a + b ) 2 + 2 ( a b ) 2 a^4 + b^4 = (a + b)^4 - 4ab(a + b)^2 + 2(ab)^2
a 4 + b 4 = ( a + b ) 4 − 4 a b ( a + b ) 2 + 2 ( a b ) 2
a 5 + b 5 = ( a + b ) 5 − 5 a b ( a + b ) 3 + 5 ( a b ) 2 ( a + b ) a^5 + b^5 = (a + b)^5 - 5ab(a + b)^3 + 5(ab)^2(a + b)
a 5 + b 5 = ( a + b ) 5 − 5 a b ( a + b ) 3 + 5 ( a b ) 2 ( a + b )
Conditional Identities
If a + b + c = 0 a + b + c = 0 a + b + c = 0
a 2 + b 2 + c 2 = − 2 ( a b + a c + b c ) a^2 + b^2 + c^2 = -2(ab + ac + bc)
a 2 + b 2 + c 2 = − 2 ( a b + a c + b c )
a 3 + b 3 + c 3 = 3 a b c a^3 + b^3 + c^3 = 3abc
a 3 + b 3 + c 3 = 3 a b c
( a b + a c + b c ) 2 = a 2 b 2 + a 2 c 2 + b 2 c 2 (ab + ac + bc)^2 = a^2b^2 + a^2c^2 + b^2c^2
( a b + a c + b c ) 2 = a 2 b 2 + a 2 c 2 + b 2 c 2
( a 2 + b 2 + c 2 ) 2 = 2 ( a 4 + b 4 + c 4 ) (a^2 + b^2 + c^2)^2 = 2(a^4 + b^4 + c^4)
( a 2 + b 2 + c 2 ) 2 = 2 ( a 4 + b 4 + c 4 )
a 4 + b 4 + c 4 = 2 ( a 2 b 2 + a 2 c 2 + b 2 c 2 ) = 1 2 ( a 2 + b 2 + c 2 ) 2 a^4 + b^4 + c^4 = 2(a^2b^2 + a^2c^2 + b^2c^2) = \frac{1}{2}(a^2 + b^2 + c^2)^2
a 4 + b 4 + c 4 = 2 ( a 2 b 2 + a 2 c 2 + b 2 c 2 ) = 2 1 ( a 2 + b 2 + c 2 ) 2
a 5 + b 5 + c 5 = − 5 a b c ( a b + b c + a c ) a^5 + b^5 + c^5 = -5abc(ab + bc + ac)
a 5 + b 5 + c 5 = − 5 a b c ( a b + b c + a c )
a 6 + b 6 + c 6 = 3 ( a b c ) 2 − 2 ( a b + b c + a c ) 3 a^6 + b^6 + c^6 = 3(abc)^2 - 2(ab + bc + ac)^3
a 6 + b 6 + c 6 = 3 ( a b c ) 2 − 2 ( a b + b c + a c ) 3
a 7 + b 7 + c 7 = 7 a b c ( a b + b c + a c ) 2 a^7 + b^7 + c^7 = 7abc(ab + bc + ac)^2
a 7 + b 7 + c 7 = 7 a b c ( a b + b c + a c ) 2
a 5 + b 5 + c 5 5 = ( a 2 + b 2 + c 2 2 ) ( a 3 + b 3 + c 3 3 ) \frac{a^5 + b^5 + c^5}{5} = \left(\frac{a^2 + b^2 + c^2}{2}\right)\left(\frac{a^3 + b^3 + c^3}{3}\right)
5 a 5 + b 5 + c 5 = ( 2 a 2 + b 2 + c 2 ) ( 3 a 3 + b 3 + c 3 )
a 6 + b 6 + c 6 = 3 ( a 3 + b 3 + c 3 3 ) 2 + 2 ( a 2 + b 2 + c 2 2 ) a^6 + b^6 + c^6 = 3\left(\frac{a^3 + b^3 + c^3}{3}\right)^2 + 2\left(\frac{a^2 + b^2 + c^2}{2}\right)
a 6 + b 6 + c 6 = 3 ( 3 a 3 + b 3 + c 3 ) 2 + 2 ( 2 a 2 + b 2 + c 2 )
a 7 + b 7 + c 7 7 = ( a 2 + b 2 + c 2 2 ) ( a 5 + b 5 + c 5 5 ) \frac{a^7 + b^7 + c^7}{7} = \left(\frac{a^2 + b^2 + c^2}{2}\right)\left(\frac{a^5 + b^5 + c^5}{5}\right)
7 a 7 + b 7 + c 7 = ( 2 a 2 + b 2 + c 2 ) ( 5 a 5 + b 5 + c 5 )
Notable Implications
If a b + b a = 2 \frac{a}{b} + \frac{b}{a} = 2 b a + a b = 2
a = b a = b
a = b
If a 2 + b 2 + c 2 = a b + a c + b c a^2 + b^2 + c^2 = ab + ac + bc a 2 + b 2 + c 2 = a b + a c + b c
a = b = c a = b = c
a = b = c
If a 3 + b 3 + c 3 = 3 a b c a^3 + b^3 + c^3 = 3abc a 3 + b 3 + c 3 = 3 a b c a + b + c = 0 a + b + c = 0 a + b + c = 0
a = b = c = 0 a = b = c = 0
a = b = c = 0
If a 2 + b 2 + c 2 + ⋯ + z 2 = 0 a^2 + b^2 + c^2 + \dots + z^2 = 0 a 2 + b 2 + c 2 + ⋯ + z 2 = 0
a = b = c = ⋯ = z = 0 a = b = c = \dots = z = 0
a = b = c = ⋯ = z = 0
If a n + b n + ⋯ + z n = 0 \sqrt[n]{a} + \sqrt[n]{b} + \dots + \sqrt[n]{z} = 0 n a + n b + ⋯ + n z = 0
a = b = ⋯ = z = 0 a = b = \dots = z = 0
a = b = ⋯ = z = 0
If x + x − 1 = a x + x^{-1} = a x + x − 1 = a
x 2 + x − 2 = a 2 − 2 x^2 + x^{-2} = a^2 - 2
x 2 + x − 2 = a 2 − 2
x 3 + x − 3 = a 3 − 3 a x^3 + x^{-3} = a^3 - 3a
x 3 + x − 3 = a 3 − 3 a
x 4 + x − 4 = ( a 2 − 2 ) 2 − 2 x^4 + x^{-4} = (a^2 - 2)^2 - 2
x 4 + x − 4 = ( a 2 − 2 ) 2 − 2
Auxiliary Identities
a 3 + b 3 + c 3 = 1 2 ( a + b + c ) [ ( a − b ) 2 + ( a − c ) 2 + ( b − c ) 2 ] a^3 + b^3 + c^3 = \frac{1}{2}(a + b + c)\left[(a - b)^2 + (a - c)^2 + (b - c)^2\right]
a 3 + b 3 + c 3 = 2 1 ( a + b + c ) [ ( a − b ) 2 + ( a − c ) 2 + ( b − c ) 2 ]
( a + b + c ) 3 − a 3 − b 3 − c 3 = 3 ( a + b ) ( b + c ) ( c + a ) (a + b + c)^3 - a^3 - b^3 - c^3 = 3(a + b)(b + c)(c + a)
( a + b + c ) 3 − a 3 − b 3 − c 3 = 3 ( a + b ) ( b + c ) ( c + a )
( a − b ) 2 + ( b − c ) 2 + ( a − c ) 2 = ( a 2 + b 2 + c 2 ) − 2 ( a b + a c + b c ) (a - b)^2 + (b - c)^2 + (a - c)^2 = (a^2 + b^2 + c^2) - 2(ab + ac + bc)
( a − b ) 2 + ( b − c ) 2 + ( a − c ) 2 = ( a 2 + b 2 + c 2 ) − 2 ( a b + a c + b c )