Vectors

Definición

Un vector es una magnitud física que se caracteriza por tener:

  • Módulo o magnitud: longitud del vector.
  • Dirección: orientación en el espacio.
  • Sentido: indica hacia dónde apunta el vector.

Se representa como:

v⃗oAB→\vec{v} \quad \text{o} \quad \overrightarrow{AB}

Representación de un vector

  • Gráficamente: mediante una flecha que va desde un punto inicial hasta un punto final.
  • Analíticamente:
    • En 2D: v⃗=(vx,vy)\vec{v} = (v_x, v_y)
    • En 3D: v⃗=(vx,vy,vz)\vec{v} = (v_x, v_y, v_z)
ʕ•̀ᴥ•́ʔ
Gráficamente
  • En 2D:

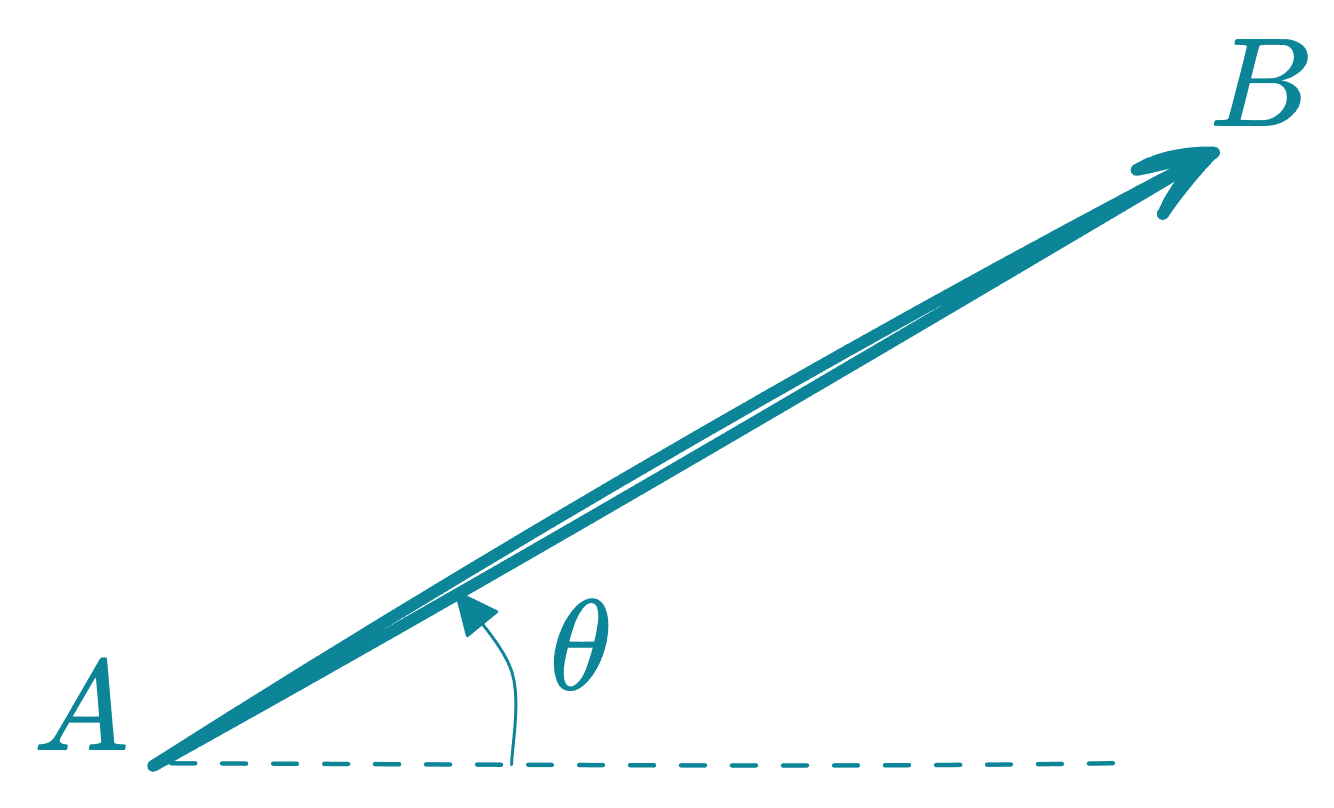
Donde:

  • AB→\overrightarrow{AB}: se lee vector AB.
  • ∣AB→∣|\overrightarrow{AB}|: se lee módulo del vector AB.
  • θ\theta: su medida nos indica la dirección del vector; se mide en sentido antihorario respecto de la horizontal (en dos dimensiones).

Tipos de vectores

Vectores colineales

Son aquellos que se encuentran contenidos en una misma línea de acción.

ʕ´•ᴥ•`ʔ
Title

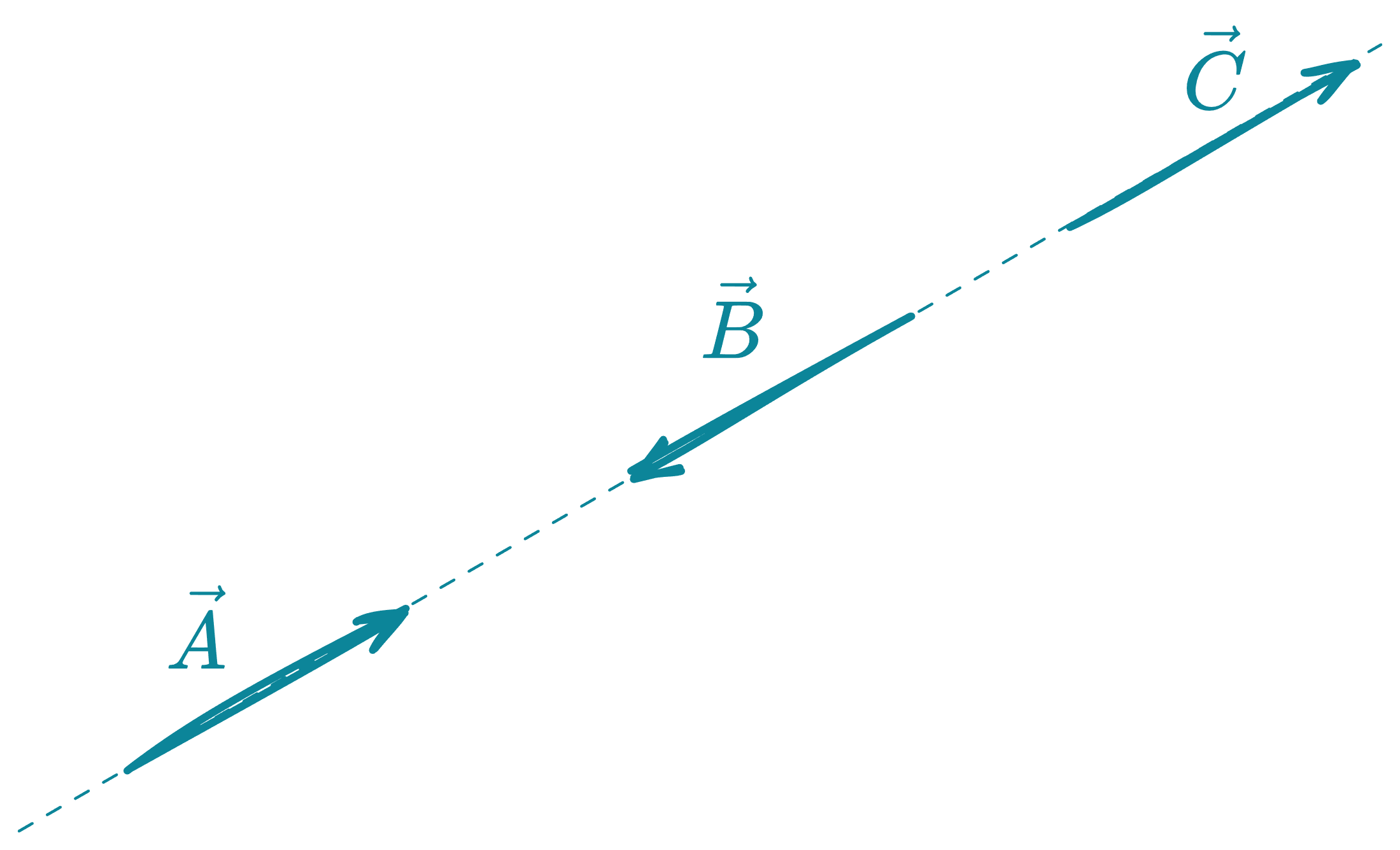
A⃗\vec{A}, B⃗\vec{B} y C⃗\vec{C} son vectores colineales porque están en una misma línea de acción.

Vectores paralelos

Son aquellos que tienen sus líneas de acción respectivamente paralelas.

ʕ´•ᴥ•`ʔ
Title

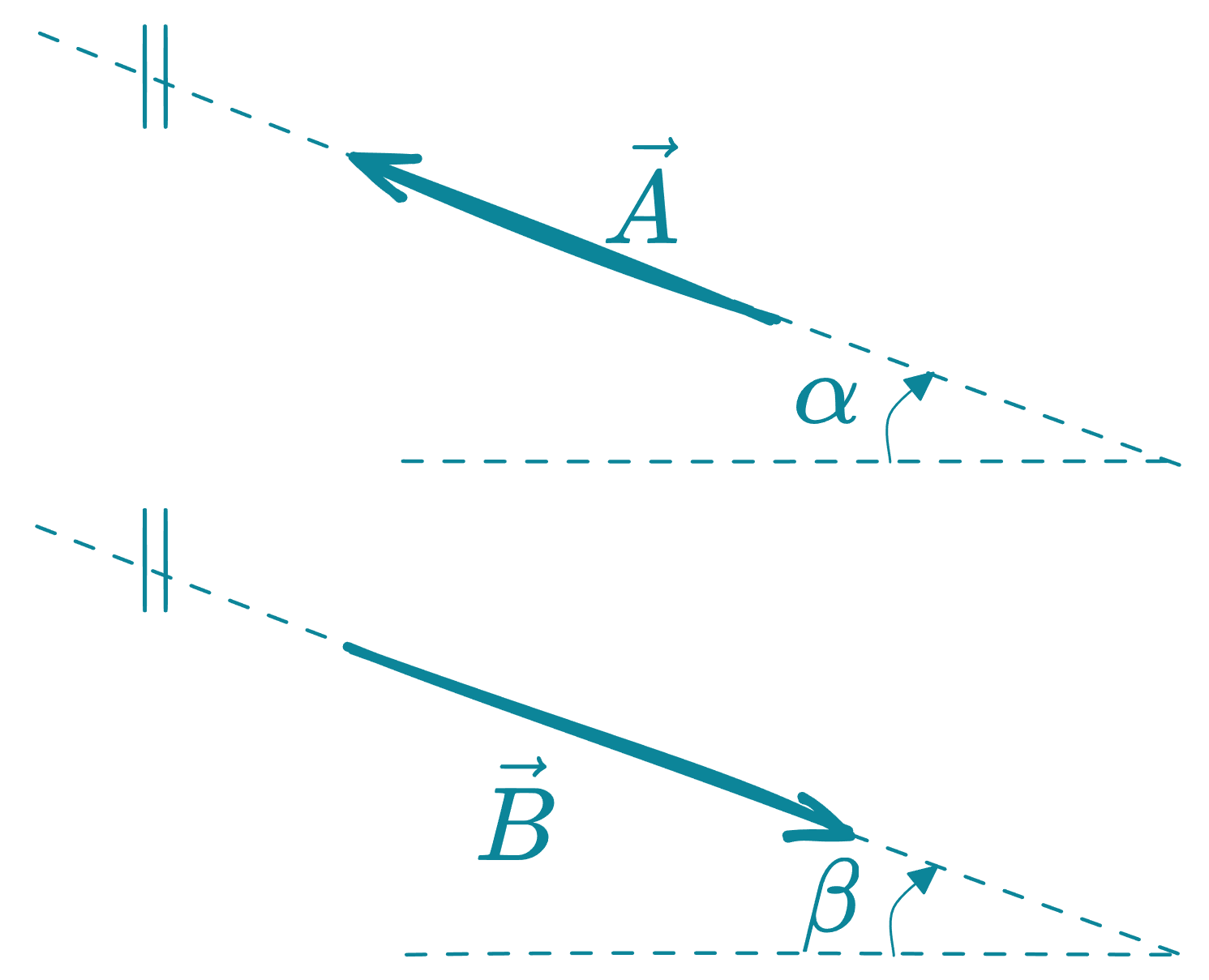
A⃗\vec{A} y B⃗\vec{B} son vectores paralelos porque sus líneas de acción son paralelas.

ʕ－ᴥ－ʔ
Nota

Podemos expresar la condición de paralelismo matemáticamente: si

α=β⇒A⃗∥B⃗\alpha = \beta \quad \Rightarrow \quad \vec{A} \parallel \vec{B}

Vectores opuestos

Son aquellos que presentan igual módulo, pero sus direcciones se diferencian en 180∘180^\circ.

ʕ´•ᴥ•`ʔ
Title

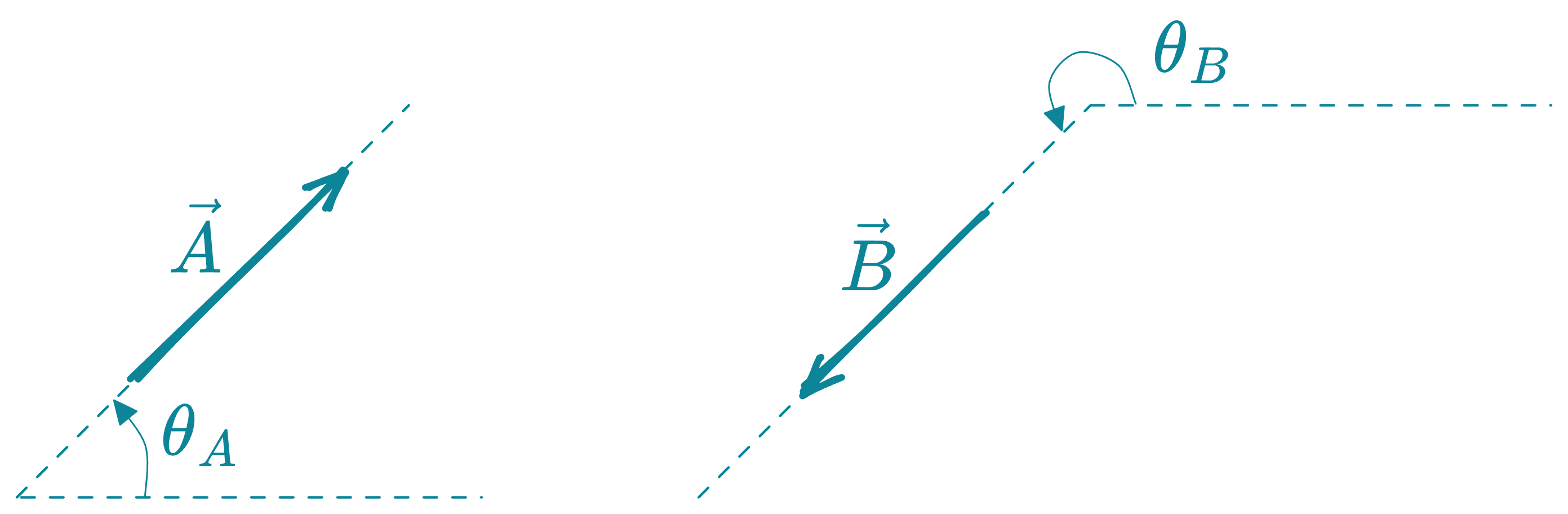
Sea

θB−θA=180∘y∣A⃗∣=∣B⃗∣\theta_B - \theta_A = 180^\circ \quad \text{y} \quad |\vec{A}| = |\vec{B}|

entonces

B⃗=−A⃗\vec{B} = -\vec{A}

B⃗\vec{B} es el opuesto de A⃗\vec{A}.

Vectores iguales

Son aquellos que presentan igual módulo e igual dirección.

ʕ－ᴥ－ʔ
Nota

Matemáticamente:
Si

∣A⃗∣=∣B⃗∣yθA=θB|\vec{A}| = |\vec{B}| \quad \text{y} \quad \theta_A = \theta_B

entonces

A⃗=B⃗;\vec{A} = \vec{B};

los vectores son iguales.

Vectores coplanares

Son aquellos que se encuentran contenidos en un mismo plano.

ʕ´•ᴥ•`ʔ
Title

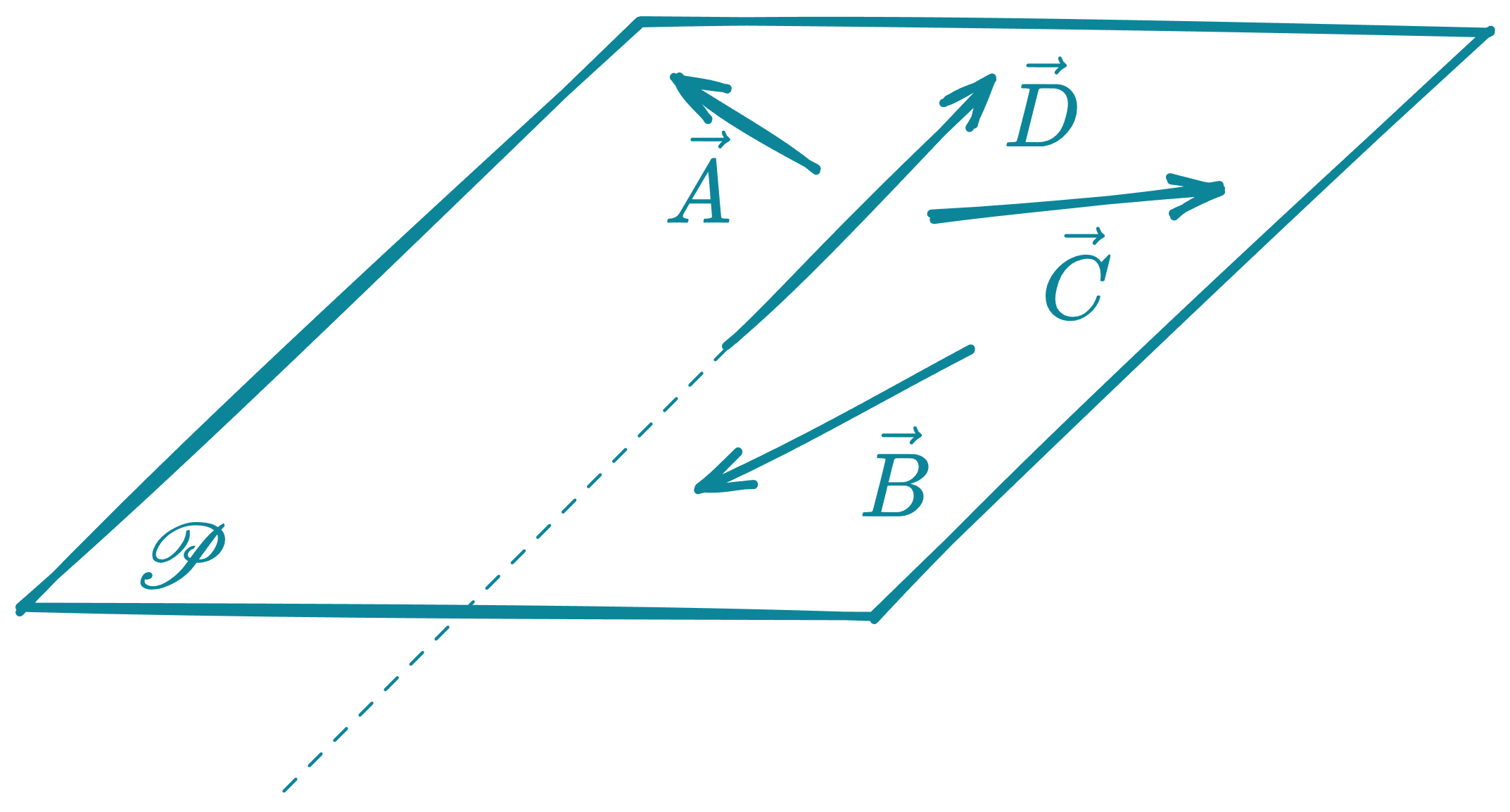
A⃗\vec{A}, B⃗\vec{B} y C⃗\vec{C} son vectores coplanares por estar en el mismo plano.

ʕ－ᴥ－ʔ
Nota

Como D⃗\vec{D} no está contenido en el plano PP, no será coplanar con los demás vectores.

Vectores concurrentes

Son aquellos cuyas líneas de acción se cortan en un mismo punto.

ʕ´•ᴥ•`ʔ
Title

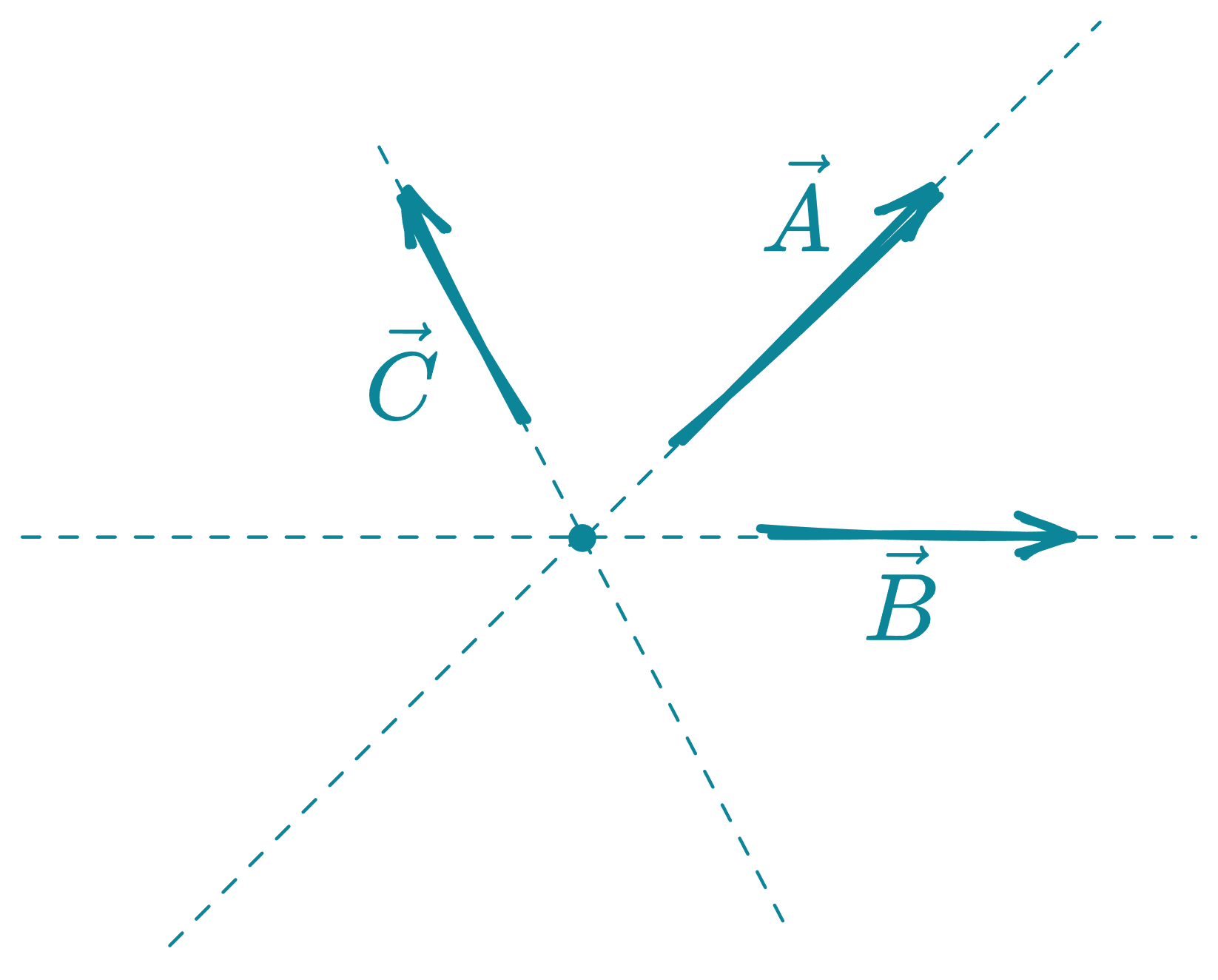
A⃗\vec{A}, B⃗\vec{B} y C⃗\vec{C} son vectores concurrentes porque todos concurren a un solo punto.

Punto de concurrencia: punto donde se intersectan las líneas de acción de los vectores.

Vector unitario (μ^\hat{\mu})

Representa la dirección de un vector cualquiera y se caracteriza porque su módulo es igual a la unidad.

ʕ´•ᴥ•`ʔ
Title

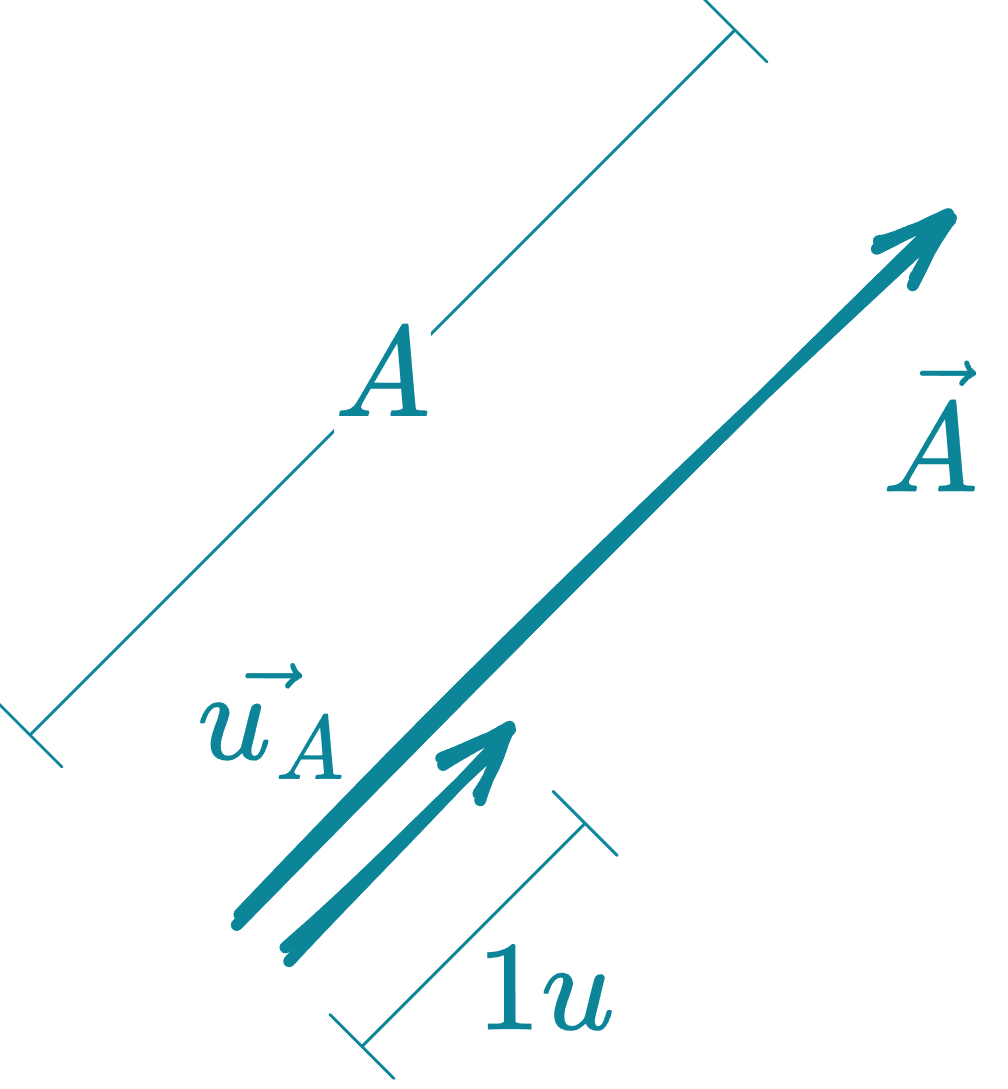
Definición matemática:

El vector unitario μ^A\hat{\mu}_A asociado a un vector A⃗\vec{A} se define como:

μ^A=A⃗∣A⃗∣\hat{\mu}_A = \frac{\vec{A}}{|\vec{A}|}

  • A⃗\vec{A}: vector original.
  • ∣A⃗∣|\vec{A}|: módulo (magnitud) del vector A⃗\vec{A}.

Propiedad fundamental:

∣μ^A∣=1 u|\hat{\mu}_A| = 1\,\text{u}

donde “u” representa la unidad de medida del sistema.

ʕ•ᴥ•ʔ
Recuerda

Un vector unitario tiene la misma dirección y sentido del vector original, pero magnitud 1.

Opearaciones con vectores

Métodos Gráficos

Método del triángulo

Nos permite hallar la resultante de dos vectores, consiste en graficar los vectores uno a continuación del otro, tal que el extremo del primero coincida con el origen del segundo vector. Su resultante se obtiene uniendo el origen del primero con el extremo del segundo vector.

Sean A⃗\vec{A} y B⃗\vec{B} los vectores.


ʕ－ᴥ－ʔ
Nota

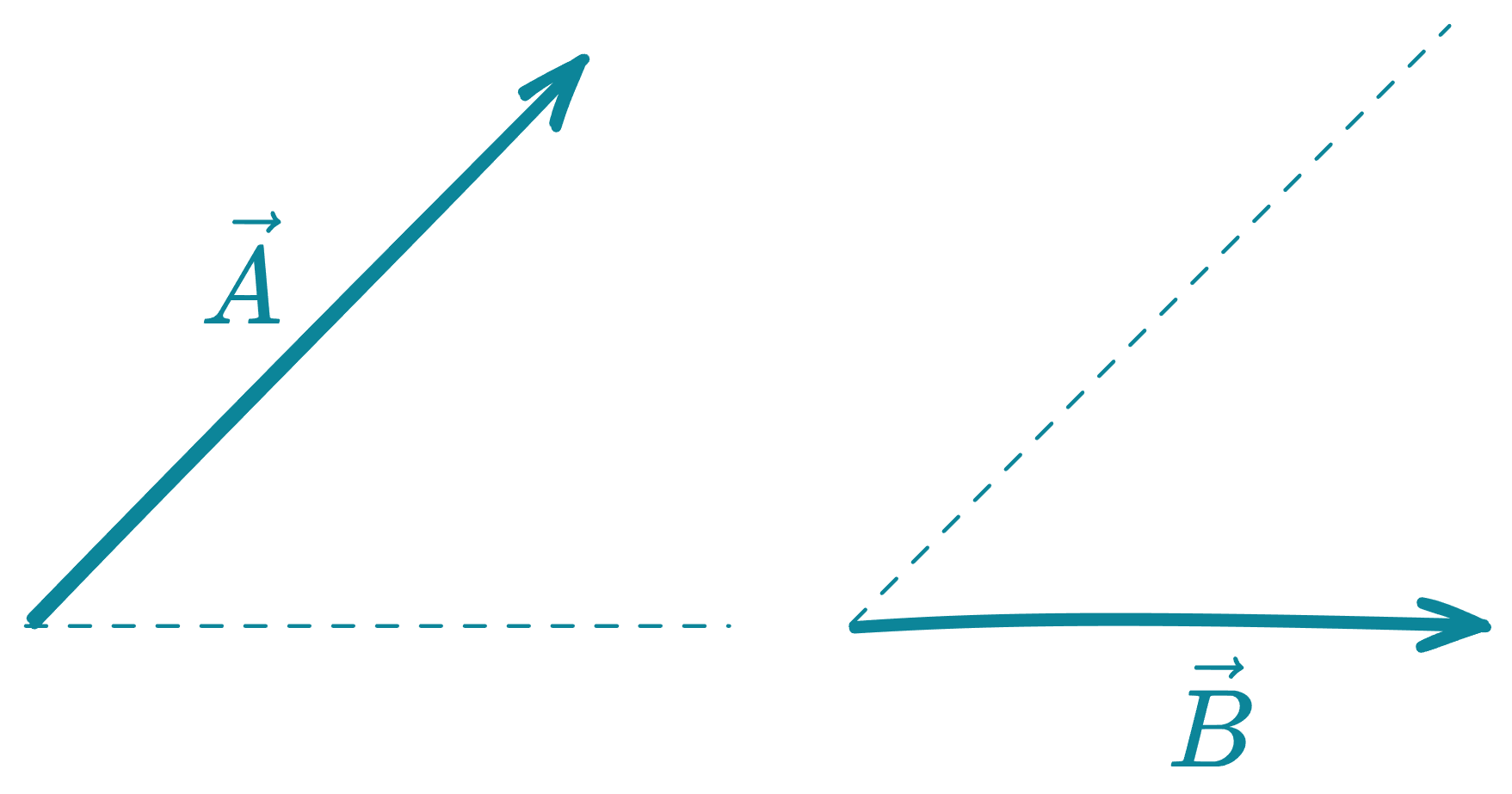
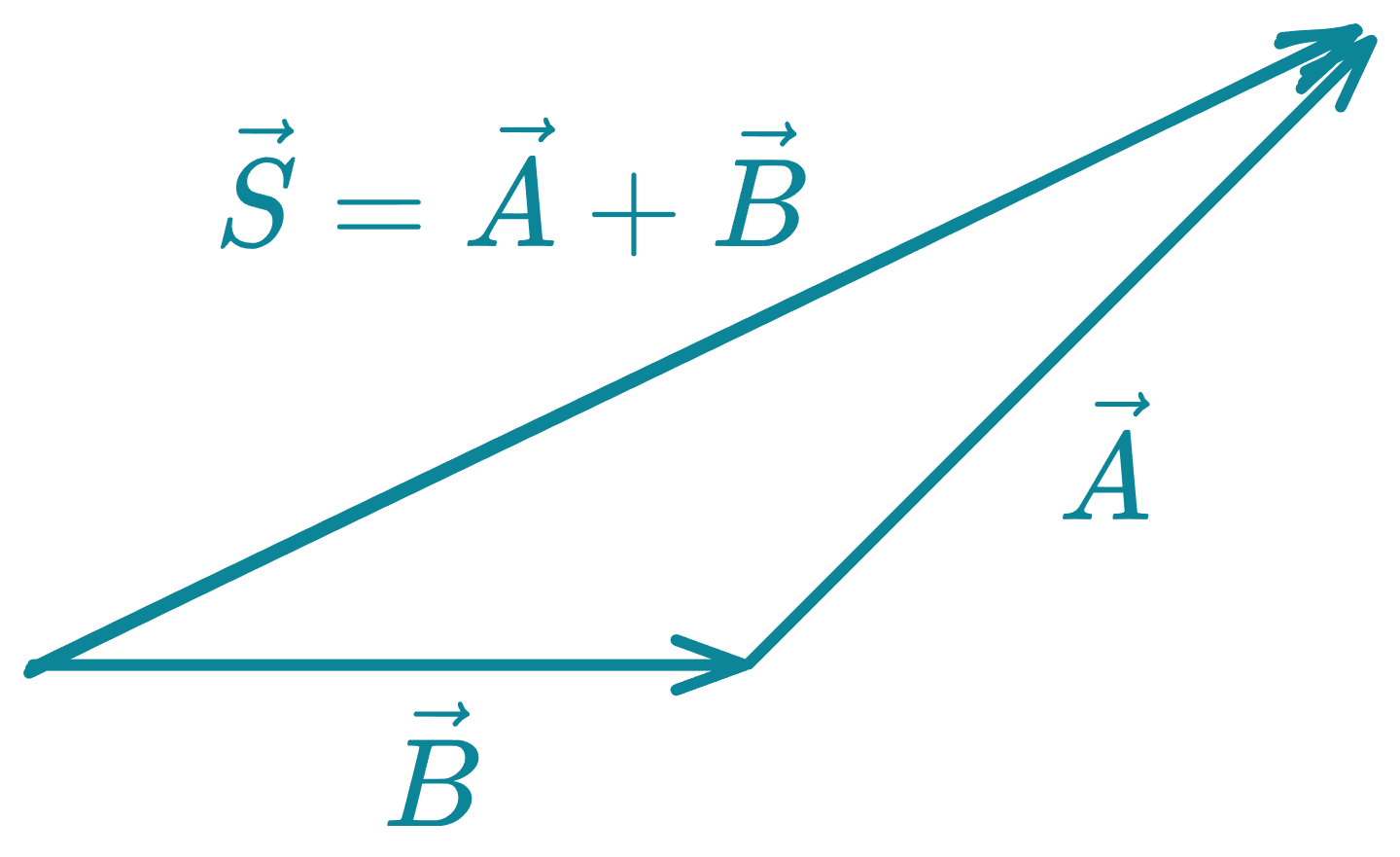
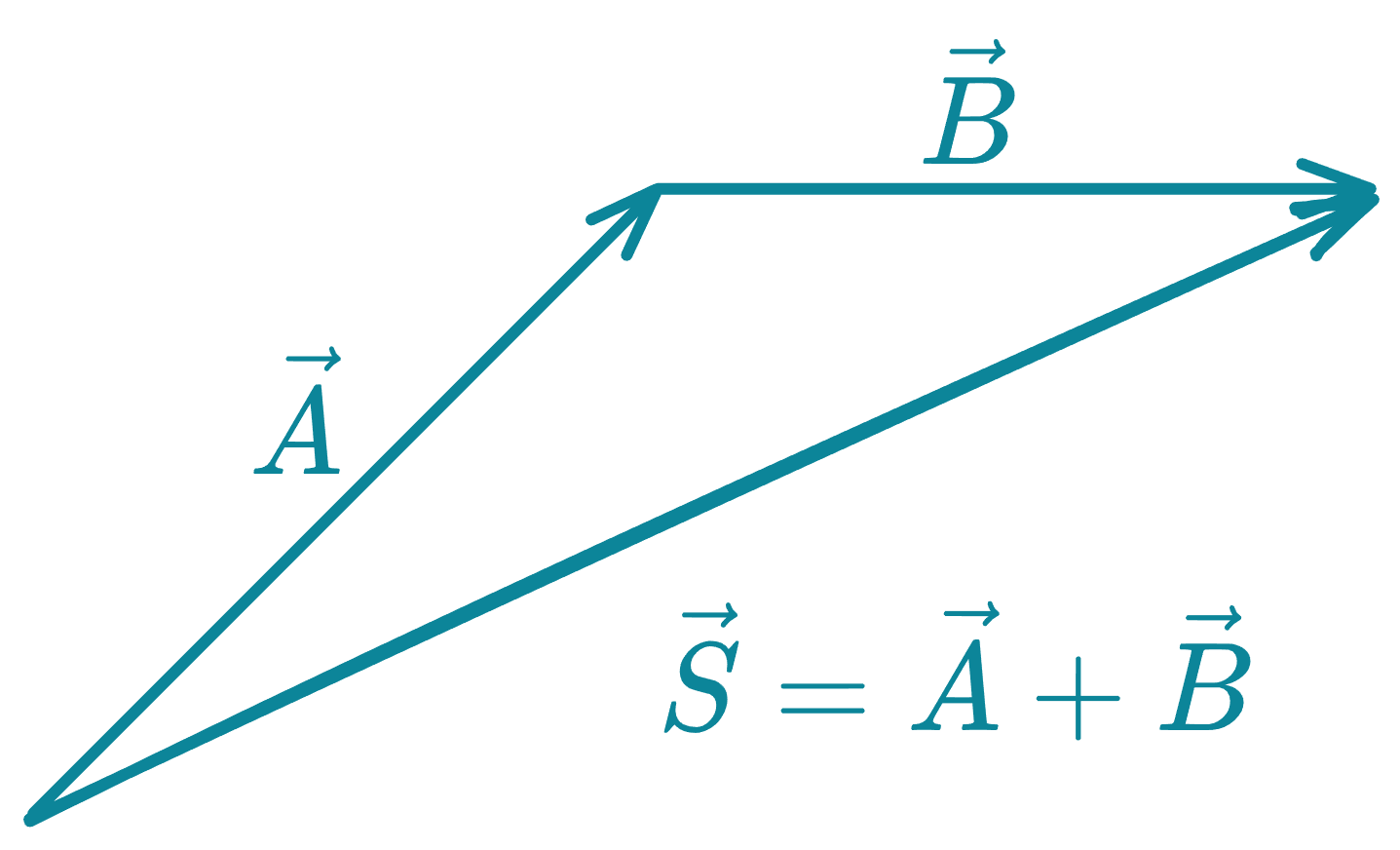
El orden de colocacion de los vectores, no altera la suma

Método del paralelogramo

Es una variante del método del triángulo, solo que en este caso debemos hacer coincidir el origen de ambos vectores y a partir de los extremos trazamos rectas paralelas a los otros vectores formando así un paralelogramo.

Sean A⃗\vec{A} y B⃗\vec{B} los vectores.

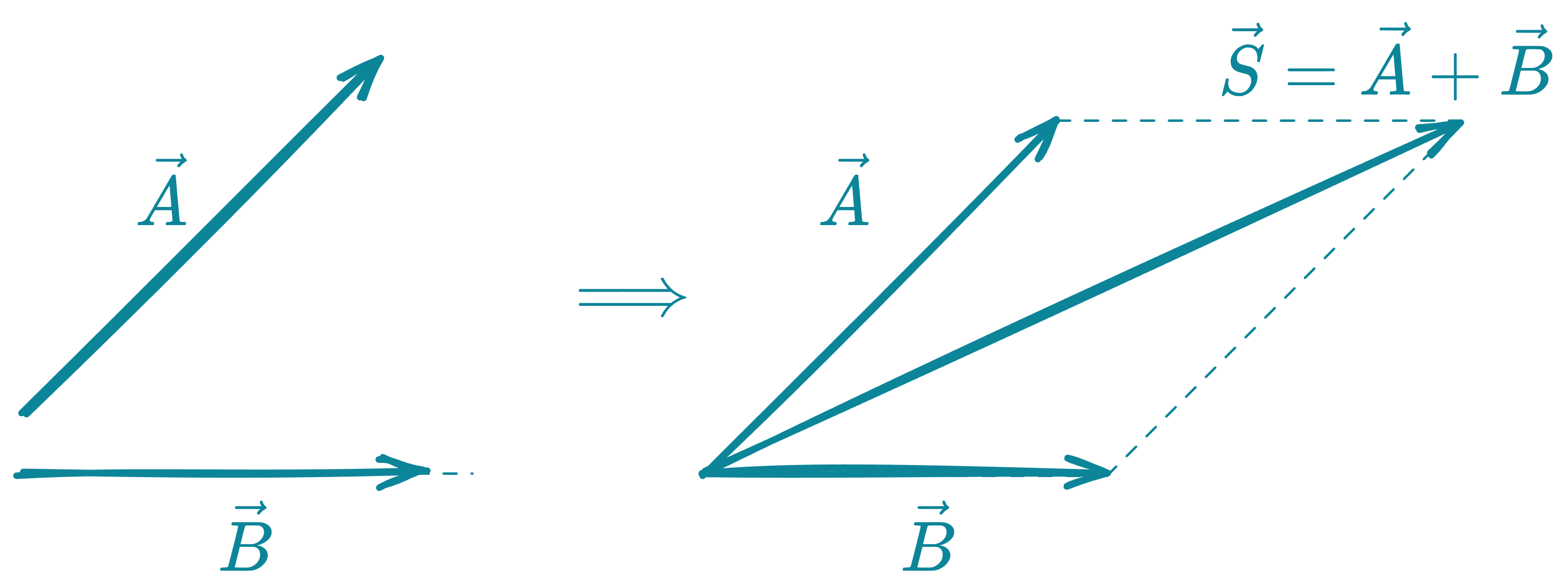
Método del polígono

Nos permite determinar la resultante de nn vectores. Consiste en colocar los vectores uno a continuación del otro, donde el vector resultante se obtiene uniendo el origen del primer vector con el extremo del último.

Sean los vectores libres.

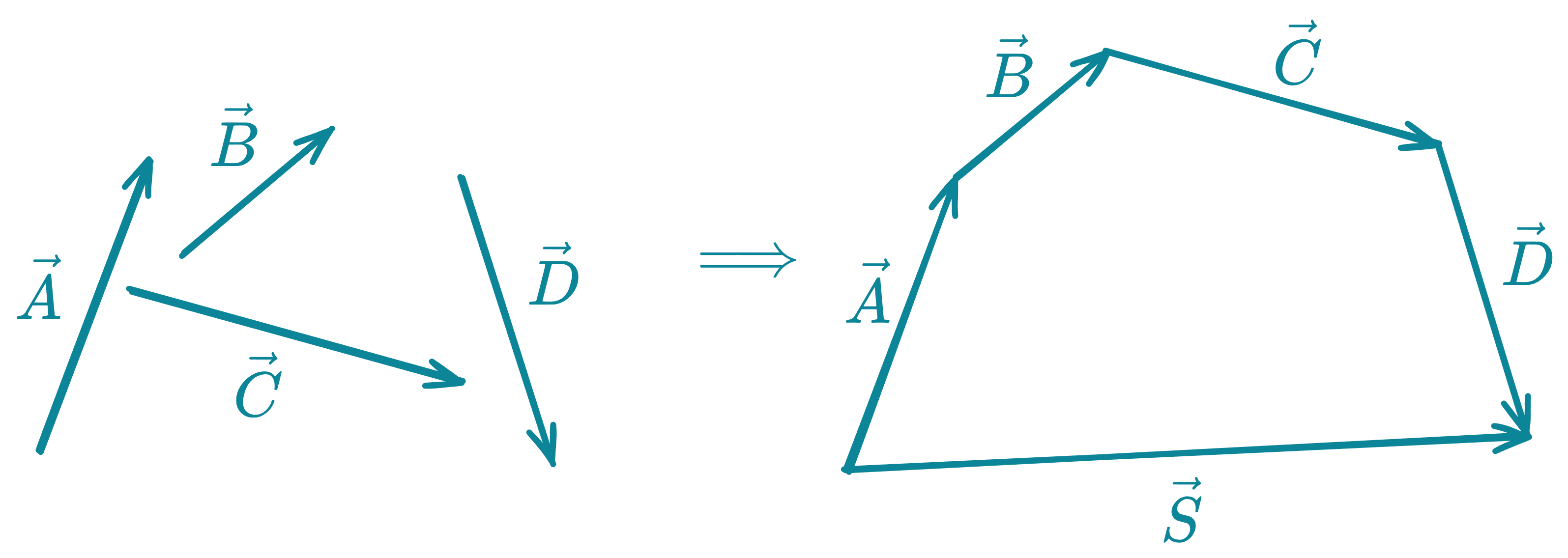
Casos Particulares

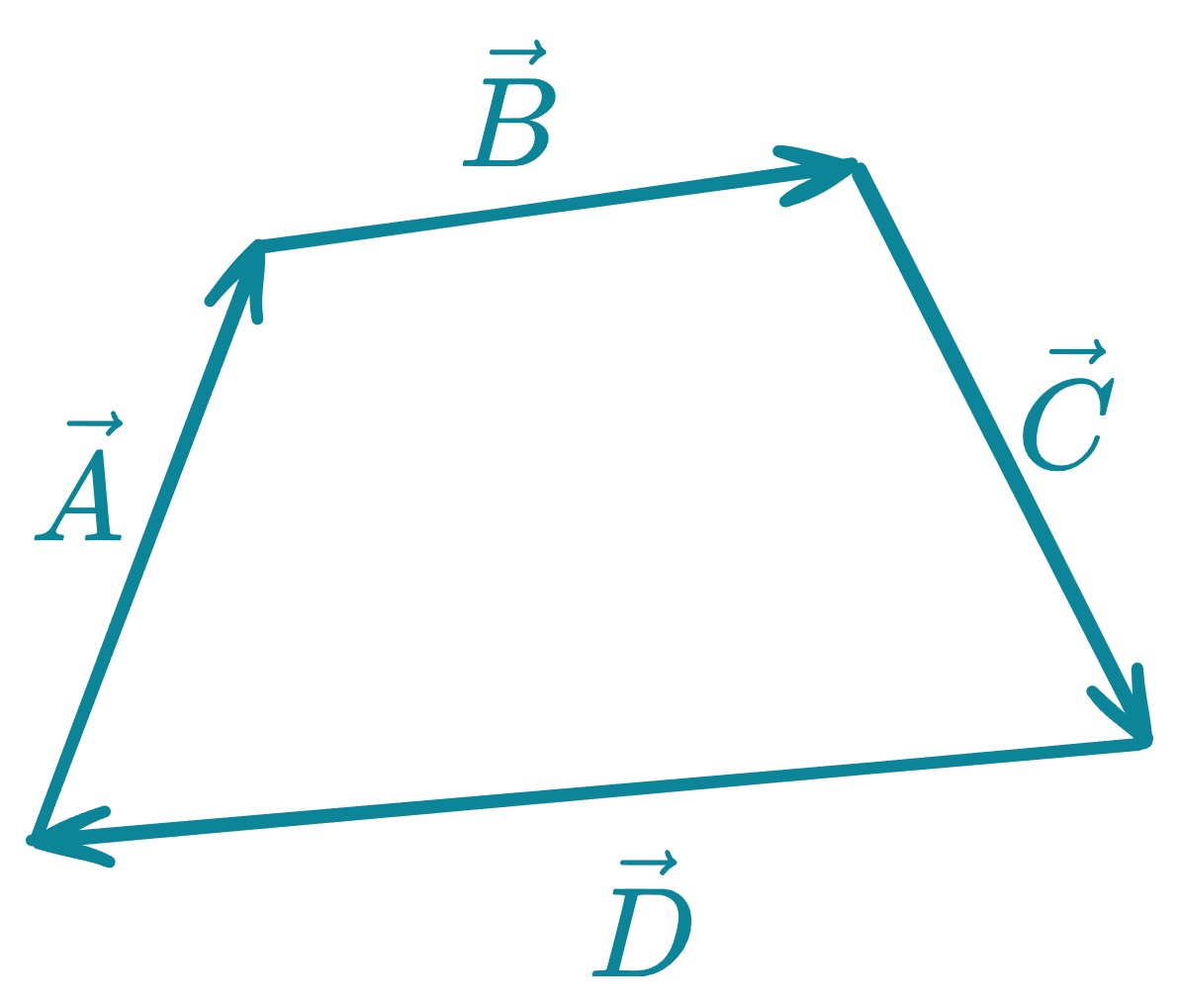
a) Vectores que forman un polígono cerrado y ordenado; la resultante es cero:

ʕ´•ᴥ•`ʔ
Title

Los vectores A⃗\vec{A}, B⃗\vec{B}, C⃗\vec{C} y D⃗\vec{D} se colocan cabeza con cola, formando un polígono cerrado. La resultante es nula:

R⃗=0⃗\vec{R} = \vec{0}

b) Vectores que forman un polígono cerrado y no ordenado; la resultante es diferente de cero:

ʕ´•ᴥ•`ʔ
Title

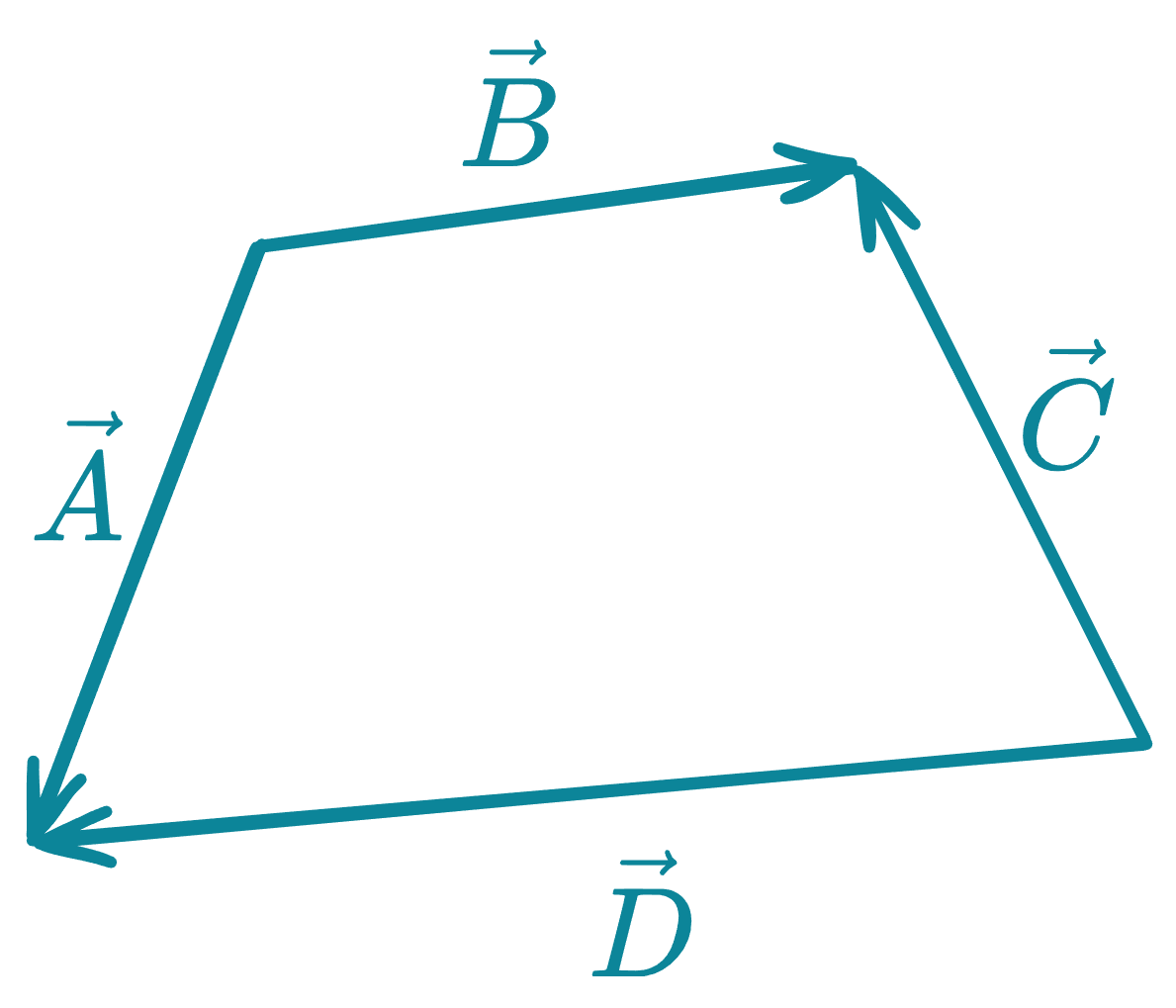
Aunque los vectores A⃗\vec{A}, B⃗\vec{B}, C⃗\vec{C} y D⃗\vec{D} forman una figura cerrada, su disposición no sigue el orden “cabeza con cola” del método del polígono. Por lo tanto, la resultante no se anula:

R⃗≠0⃗\vec{R} \neq \vec{0}

Métodos Analíticos

Método del triángulo

Podemos resolver un triángulo vectorial si conocemos algunos de sus lados y ángulos, usando la ley de senos.

ʕ´•ᴥ•`ʔ
Title

Sean A⃗\vec{A}, B⃗\vec{B} y C⃗\vec{C} vectores que forman un triángulo, cuyos módulos son AA, BB y CC, y cuyos ángulos opuestos son α\alpha, β\beta y γ\gamma respectivamente.

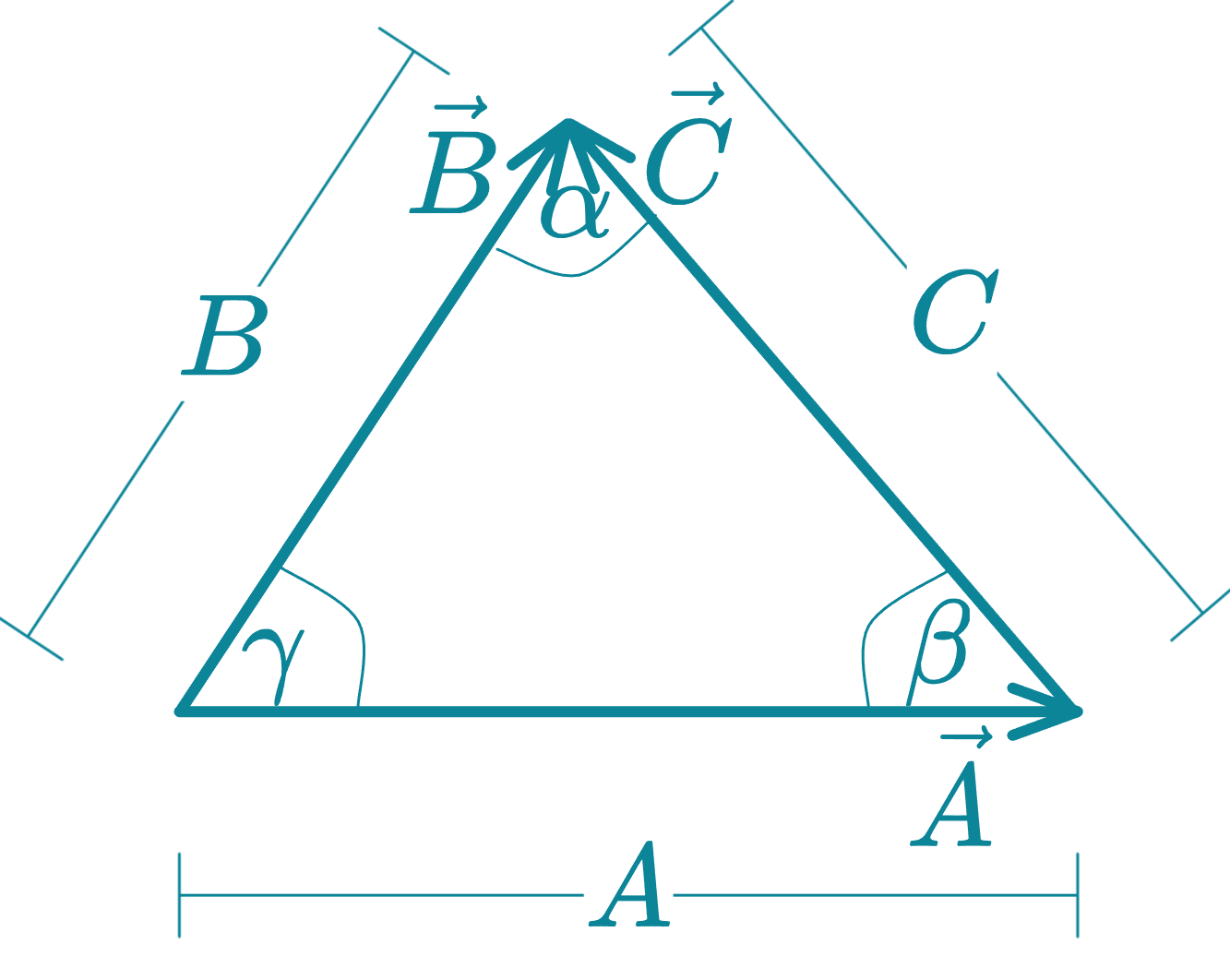
I. Ley de senos

Asin⁡α=Bsin⁡β=Csin⁡γ\frac{A}{\sin \alpha} = \frac{B}{\sin \beta} = \frac{C}{\sin \gamma}

II. Ley de cosenos

A2=B2+C2−2BCcos⁡αB2=A2+C2−2ACcos⁡βC2=A2+B2−2ABcos⁡γ\begin{align*} A^2 &= B^2 + C^2 - 2BC \cos \alpha \\ B^2 &= A^2 + C^2 - 2AC \cos \beta \\ C^2 &= A^2 + B^2 - 2AB \cos \gamma \end{align*}

equationzone.com