The Straight Line

Definition

A straight line is the locus of all points in the plane that follow a constant direction.

Angle of Inclination

The angle of inclination $\theta$ of a line is the angle measured counterclockwise from the positive $x$-axis to the line, such that $0^\circ \leq \theta < 180^\circ$.

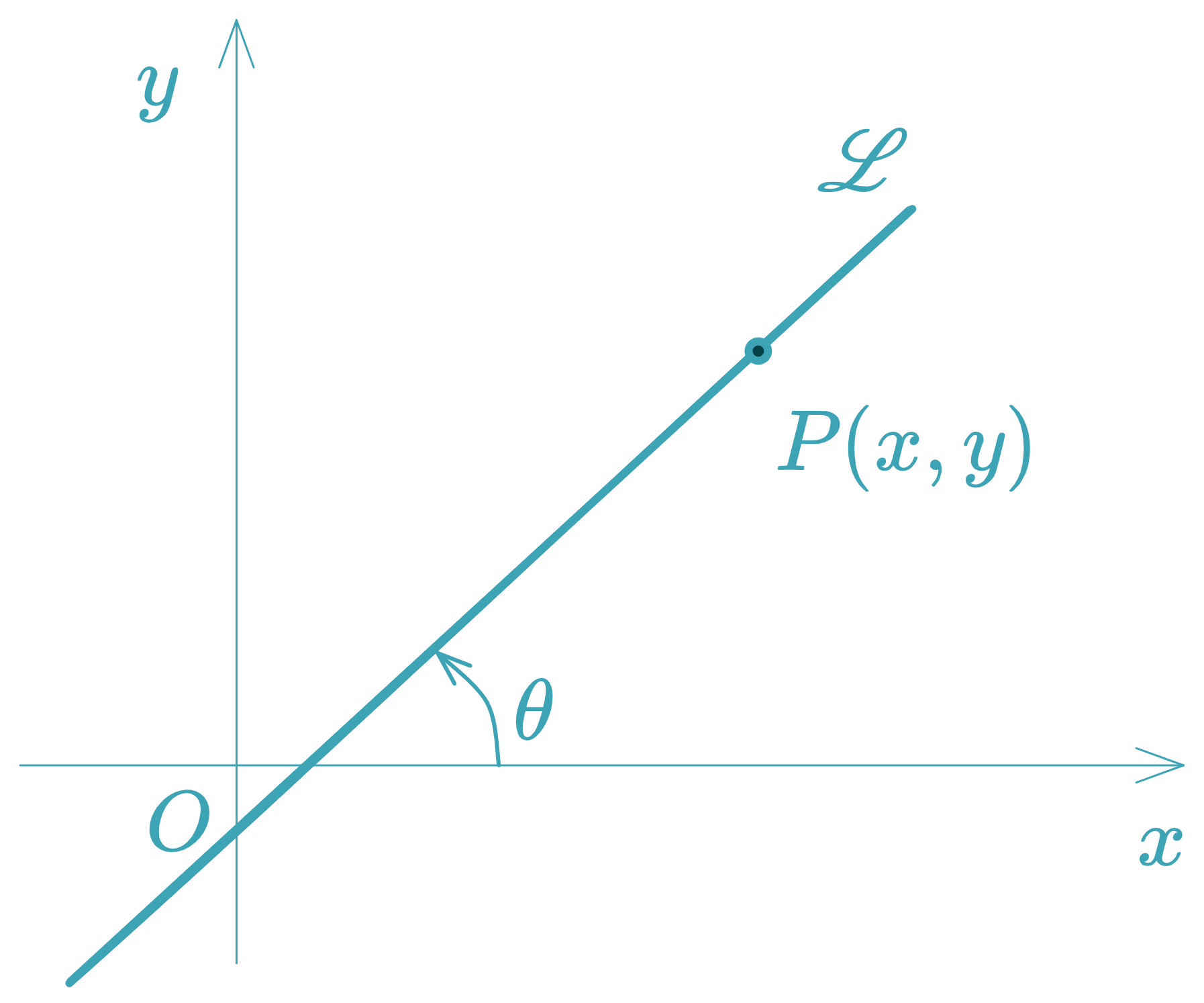
Slope of a Line

The slope $m$ of a line is defined as the tangent of its angle of inclination:

$$\boxed{m = \tan \theta}$$

Observations:
1. If $\theta < 90^\circ$, then $m > 0$ → the line is **increasing**.  
![Positive slope - equationzone.com](https://res.cloudinary.com/dno4gyfgn/image/upload/v1754918270/obsidian/math/analytic-geometry/straight-line/79152cb167099c92eaa01cef138017cb.png)
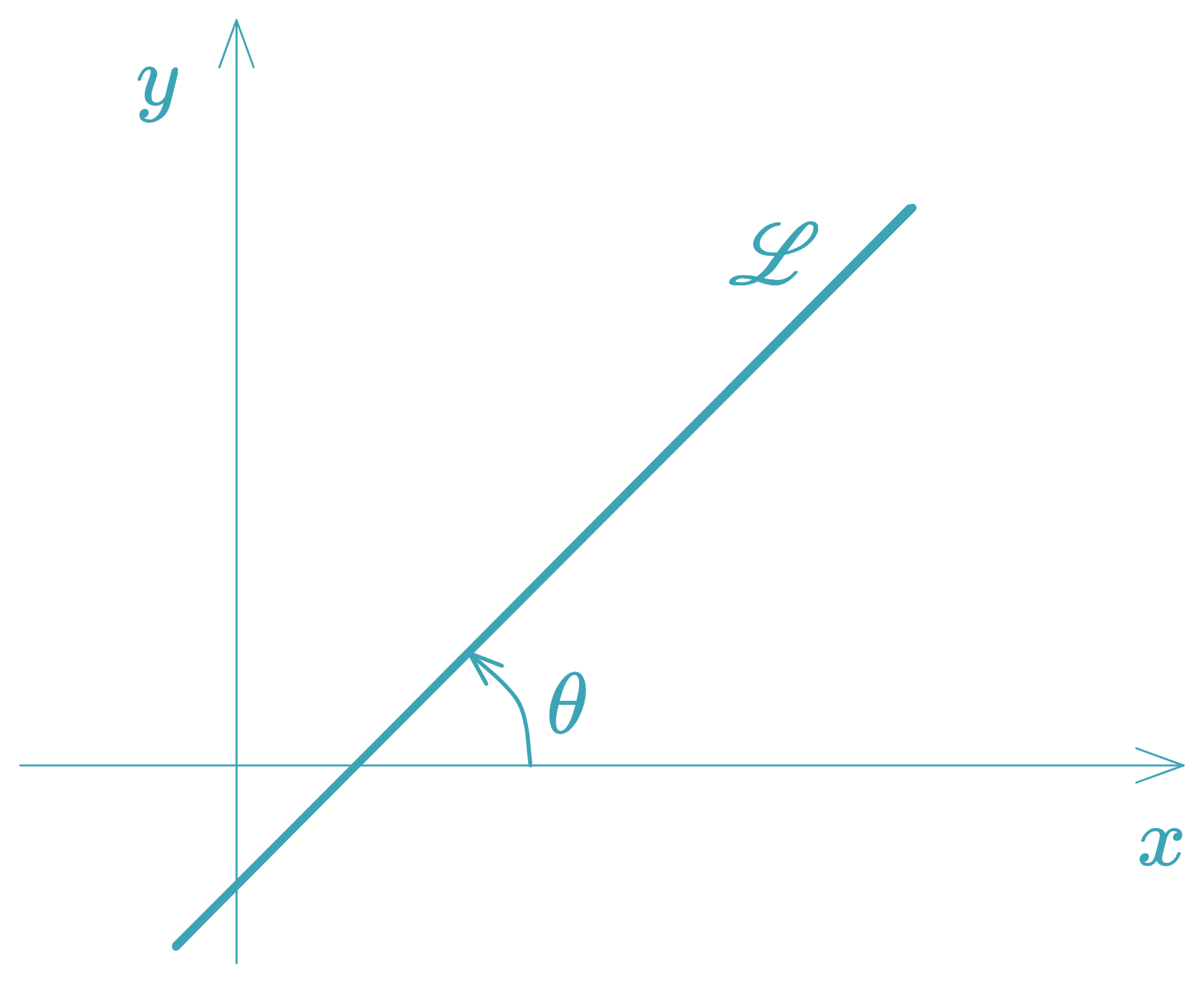
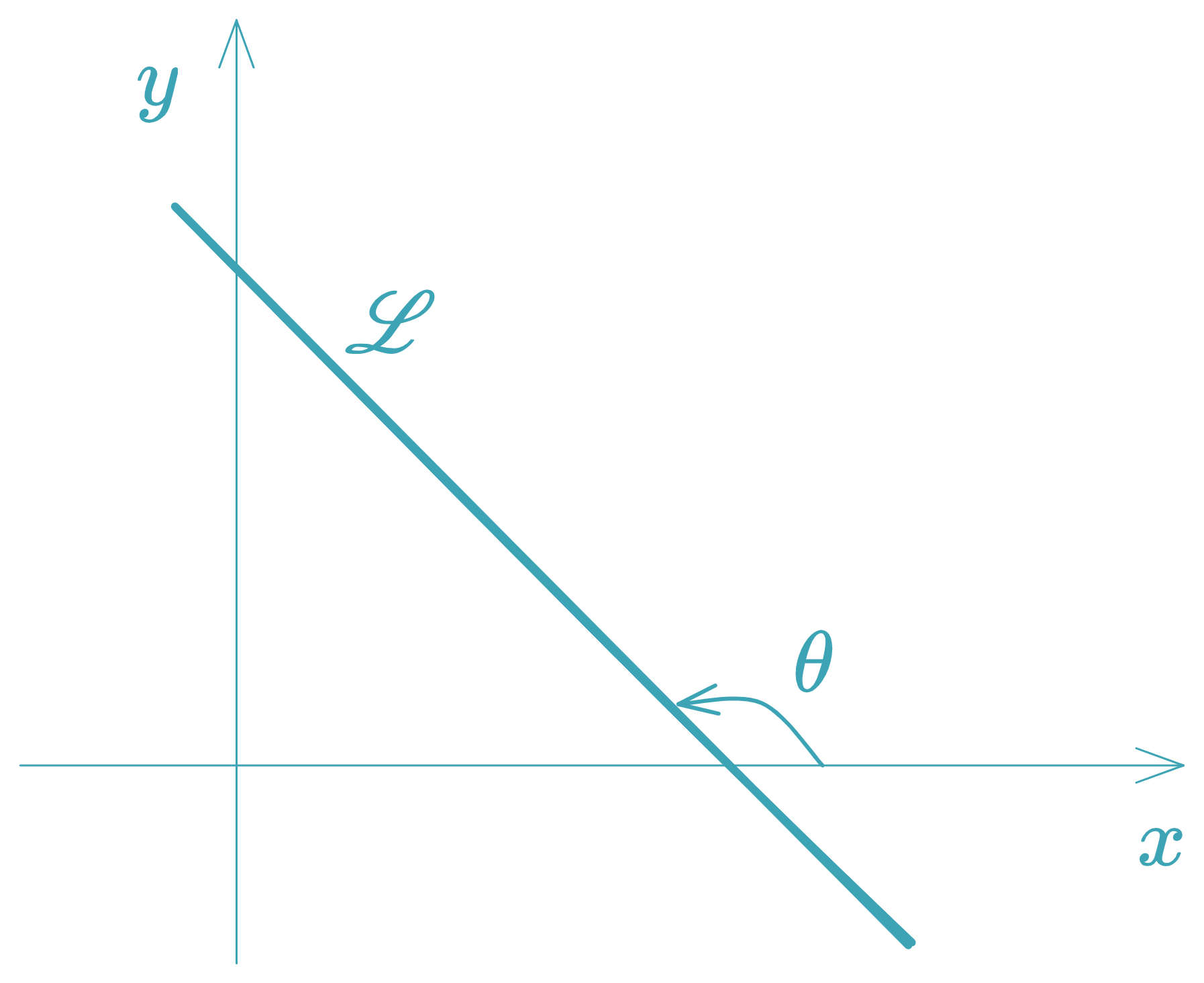
2. If $\theta > 90^\circ$, then $m < 0$ → the line is **decreasing**.  
![Negative slope - equationzone.com](https://res.cloudinary.com/dno4gyfgn/image/upload/v1754918322/obsidian/math/analytic-geometry/straight-line/58bbd0a27ccd5d0bd67def627936bfcb.png)
3. If $\theta = 90^\circ$, then $m$ is **undefined** → the line is **vertical**.

---

Forms of the Equation of a Line

Point-Slope Form

Given a point $P_1(x_1, y_1)$ and a slope $m$:

$$y - y_1 = m(x - x_1)$$

---

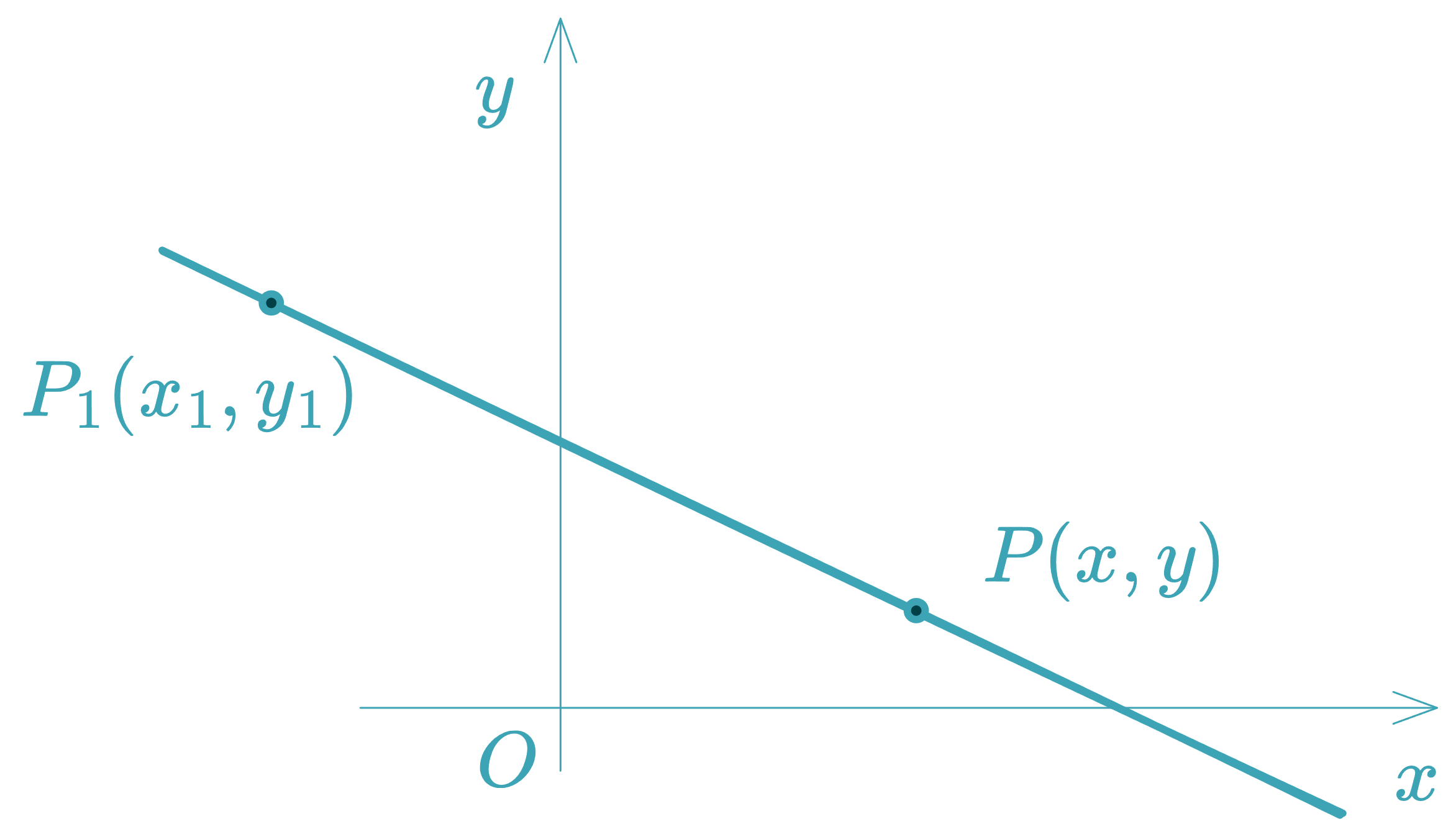
Two-Point Form (Cartesian Form)

Given two distinct points $P_1(x_1, y_1)$ and $P_2(x_2, y_2)$, with $x_1 \ne x_2$:

$$y - y_1 = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1)$$

---

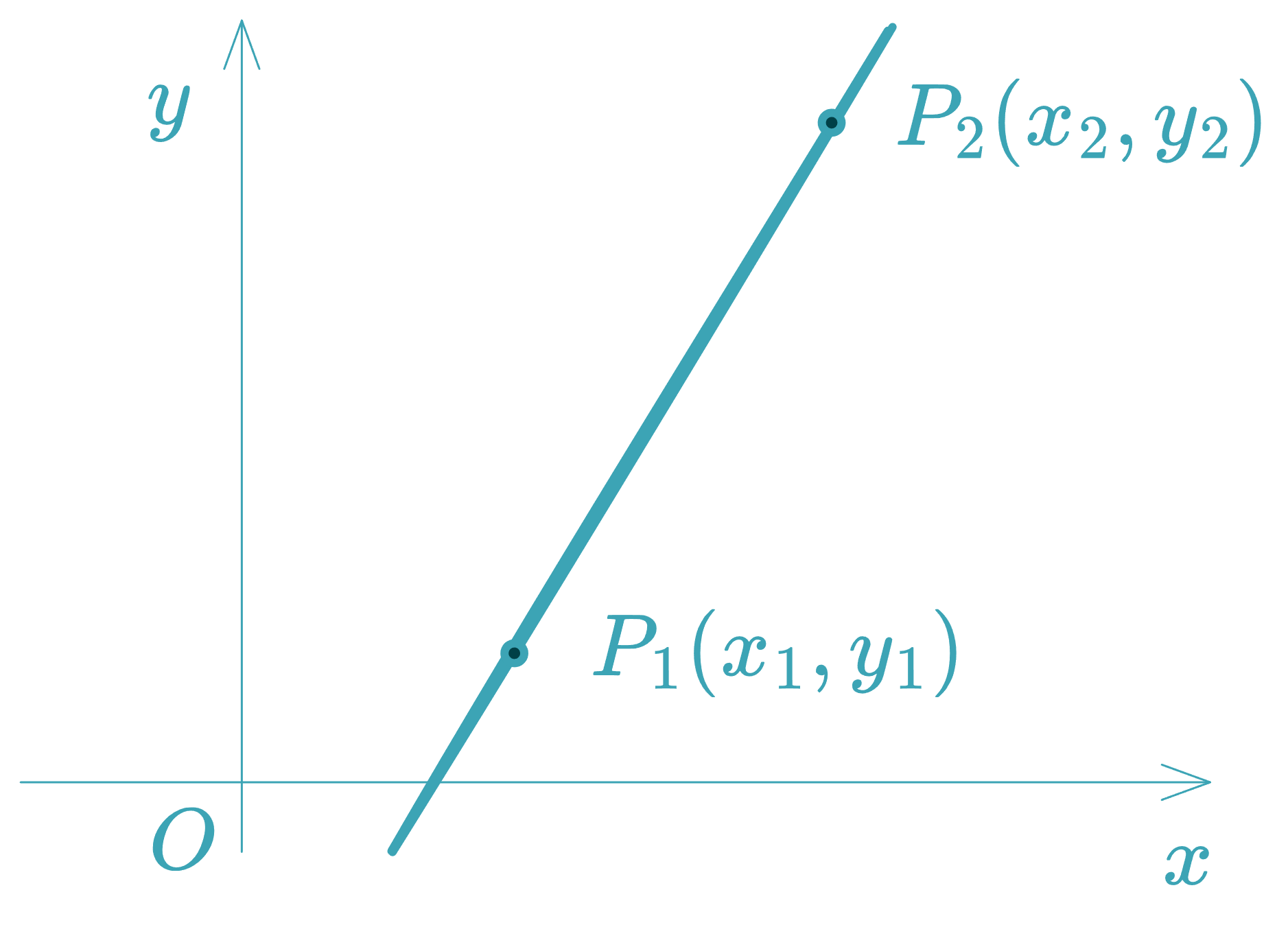
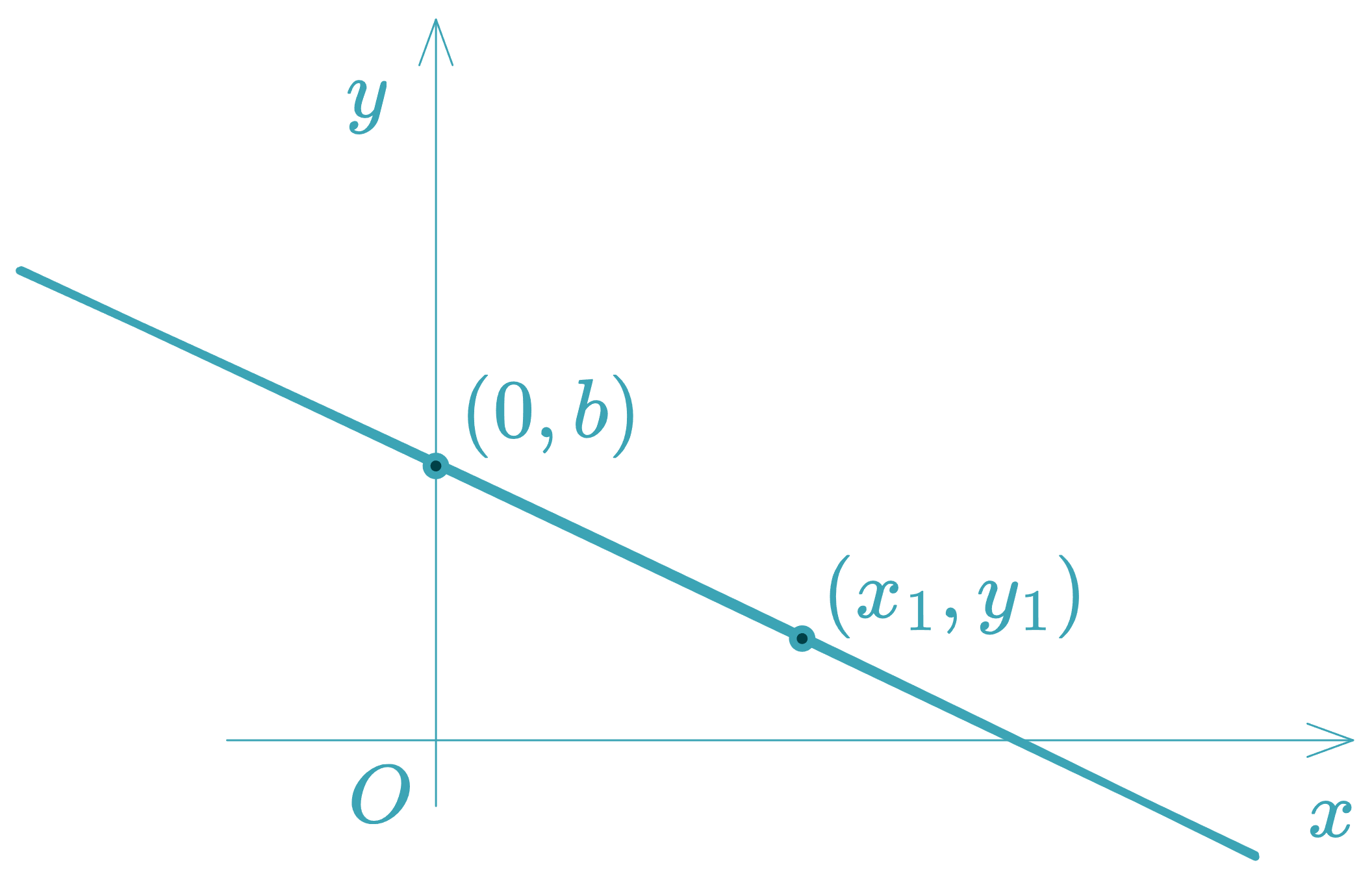
Slope–Intercept Form

Given slope $m$ and $y$-intercept $b$ (the point where the line crosses the $y$-axis):

$$y = mx + b$$

Where:

• $m$: slope
• $b$: $y$-intercept

---

Intercept Form (Symmetric Form)

If the line intersects the $x$-axis at $(a, 0)$ and the $y$-axis at $(0, b)$, with $a \ne 0$ and $b \ne 0$:

$$\frac{x}{a} + \frac{y}{b} = 1$$

Where:

• $a$: $x$-intercept
• $b$: $y$-intercept

---

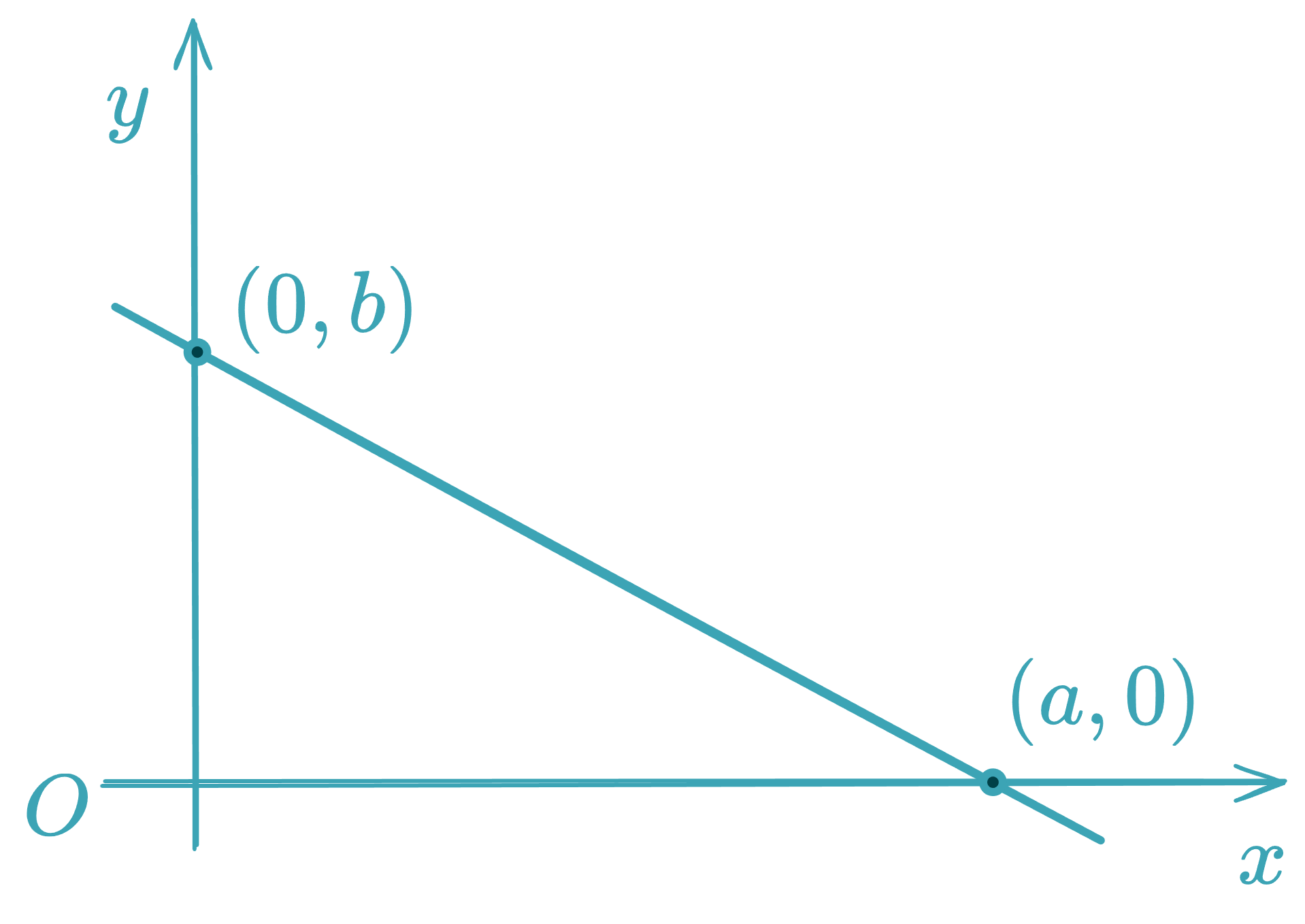
General Form of the Equation of a Line

Any straight line can be written as:

$$\boxed{Ax + By + C = 0}$$

where $A, B, C \in \mathbb{R}$, and not all are zero.

Special Cases:
1. If $A = 0$, $B \ne 0$, $C \ne 0$:  
   $\Rightarrow y = -\dfrac{C}{B}$ → **horizontal line** (parallel to the $x$-axis).
2. If $B = 0$, $A \ne 0$, $C \ne 0$:  
   $\Rightarrow x = -\dfrac{C}{A}$ → **vertical line** (parallel to the $y$-axis).
3. If $A \ne 0$, $B \ne 0$:  
   $\Rightarrow y = -\dfrac{A}{B}x - \dfrac{C}{B}$ → slope–intercept form, with slope $m = -\dfrac{A}{B}$.

---

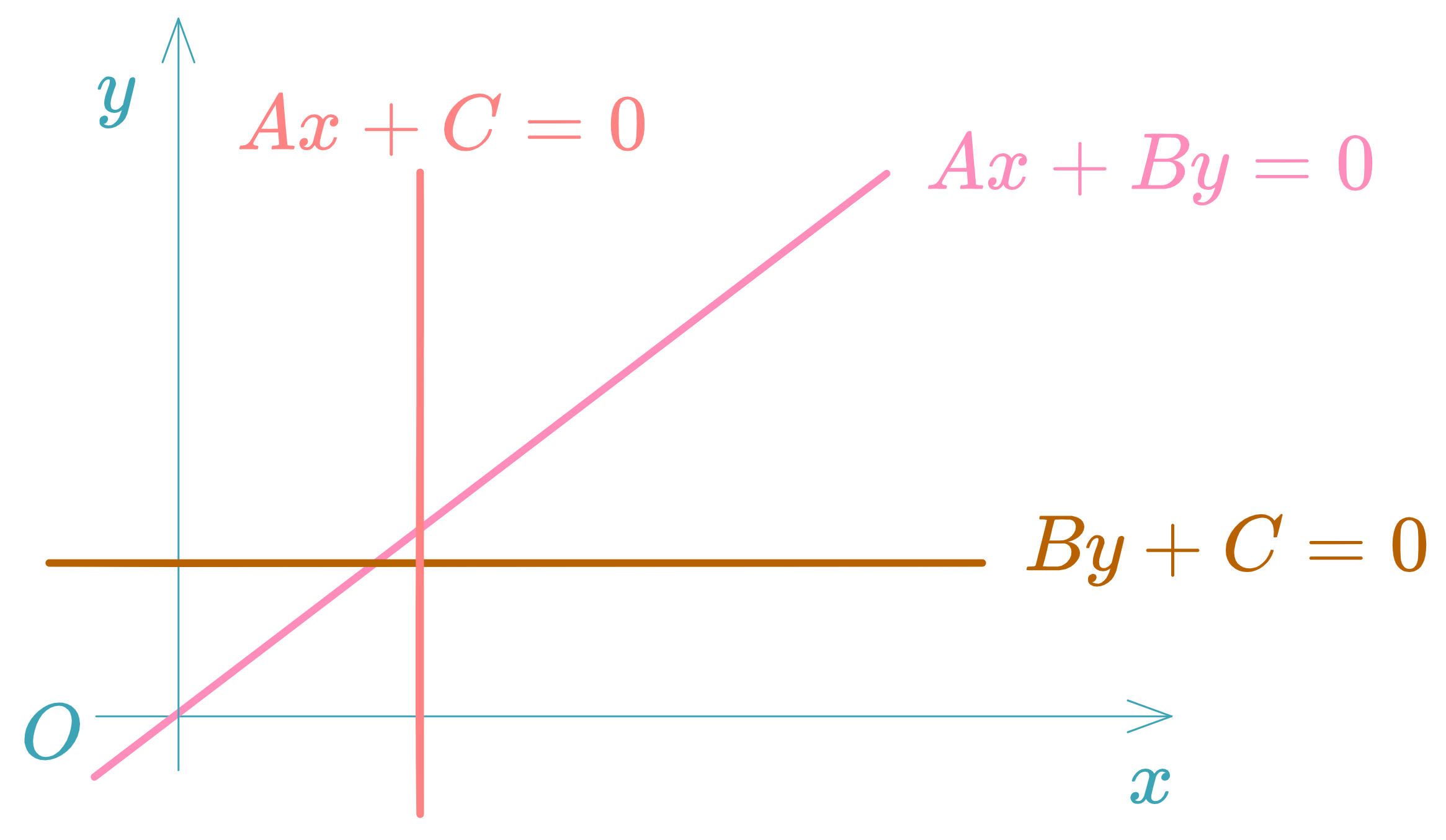
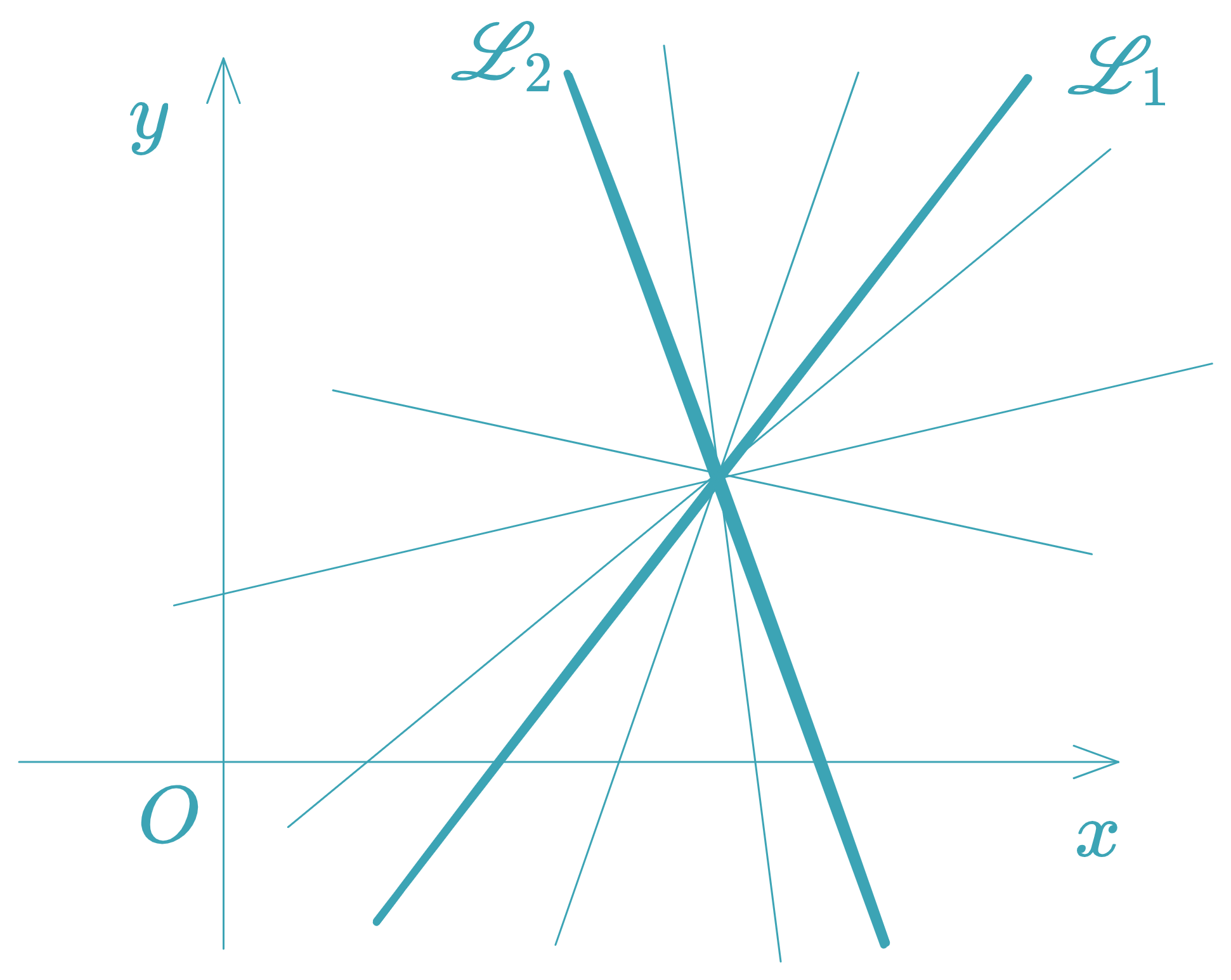
Angle Between Two Lines

Given two lines with slopes $m_1$ and $m_2$, the acute angle $\theta$ between them is:

$$\tan \theta = \left| \frac{m_2 - m_1}{1 + m_1 m_2} \right|$$

title: Note:
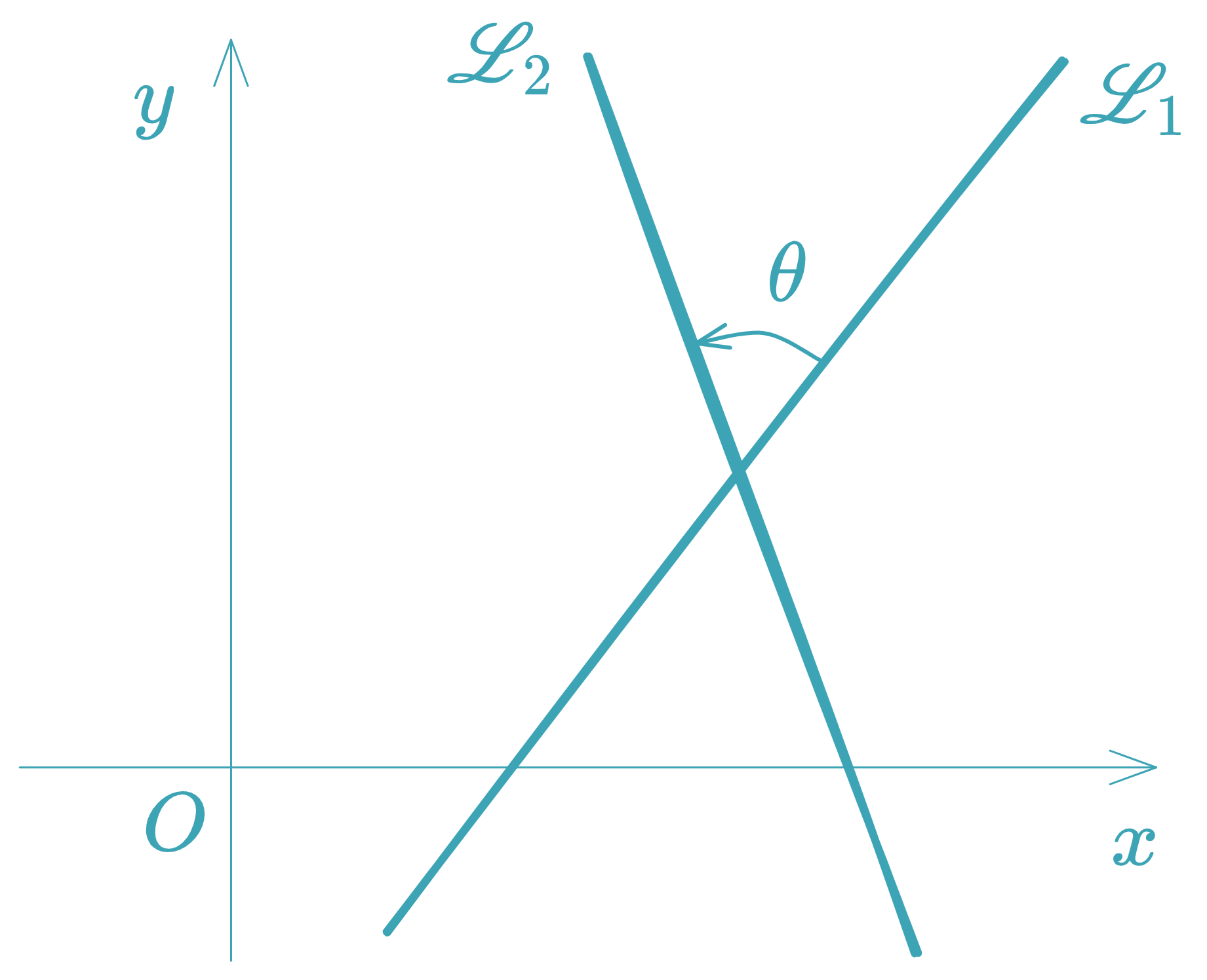
This formula gives the **acute angle** between the lines. For the obtuse angle, use $180^\circ - \theta$.

---

Relative Positions of Two Lines

Consider the lines:

$$\begin{aligned} \mathscr{L}_1 &: A_1x + B_1y + C_1 = 0 \\ \mathscr{L}_2 &: A_2x + B_2y + C_2 = 0 \end{aligned}$$

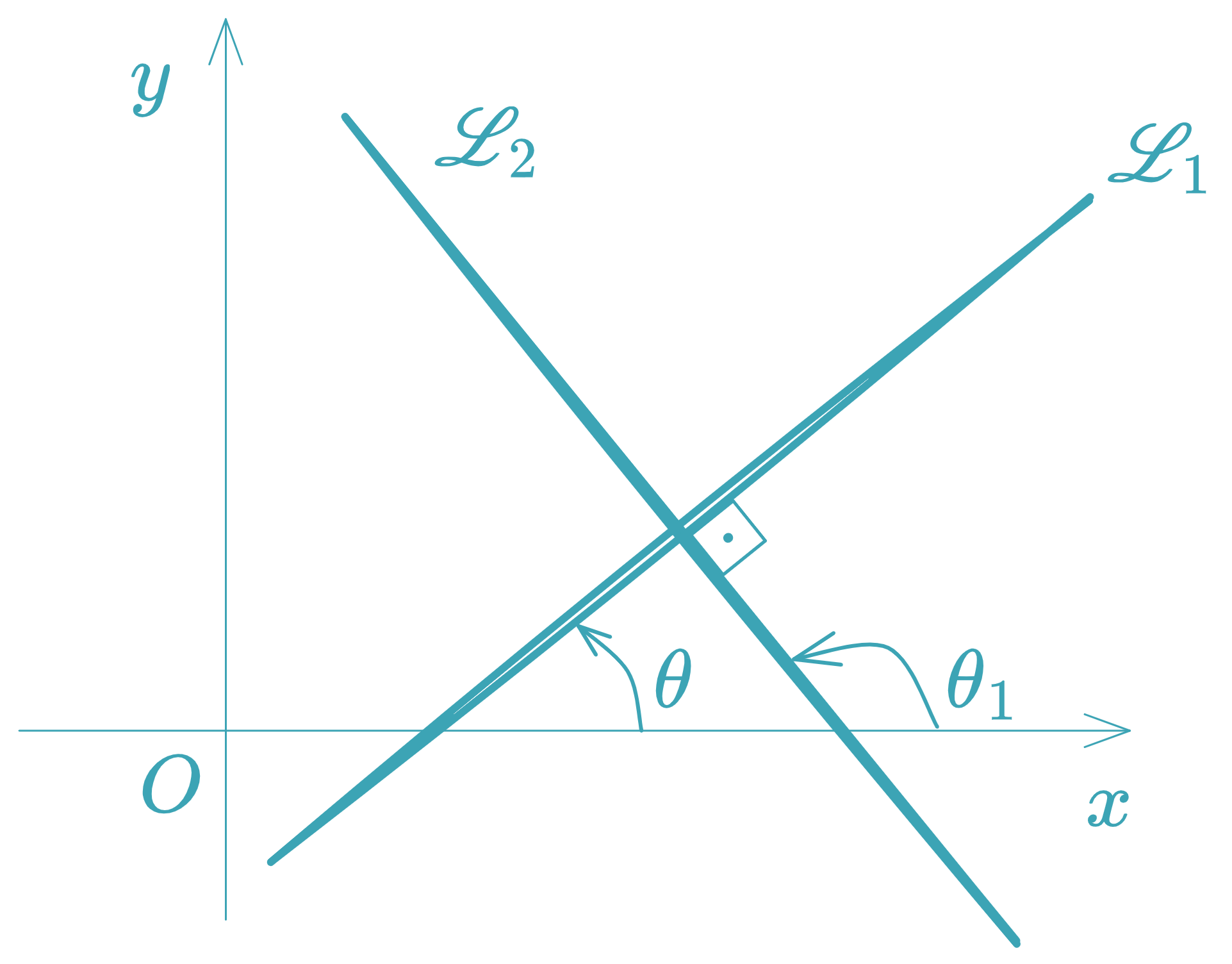
Perpendicular Lines

Two lines are perpendicular if their slopes satisfy $m_1 \cdot m_2 = -1$. In terms of coefficients:

$$\boxed{A_1 A_2 + B_1 B_2 = 0}$$

---

Parallel Lines

Two lines are parallel if they have equal slopes:

$$m_1 = m_2 \quad \Rightarrow \quad \boxed{\frac{A_1}{A_2} = \frac{B_1}{B_2}} \quad \text{(provided } A_2, B_2 \ne 0\text{)}$$

title: Note:
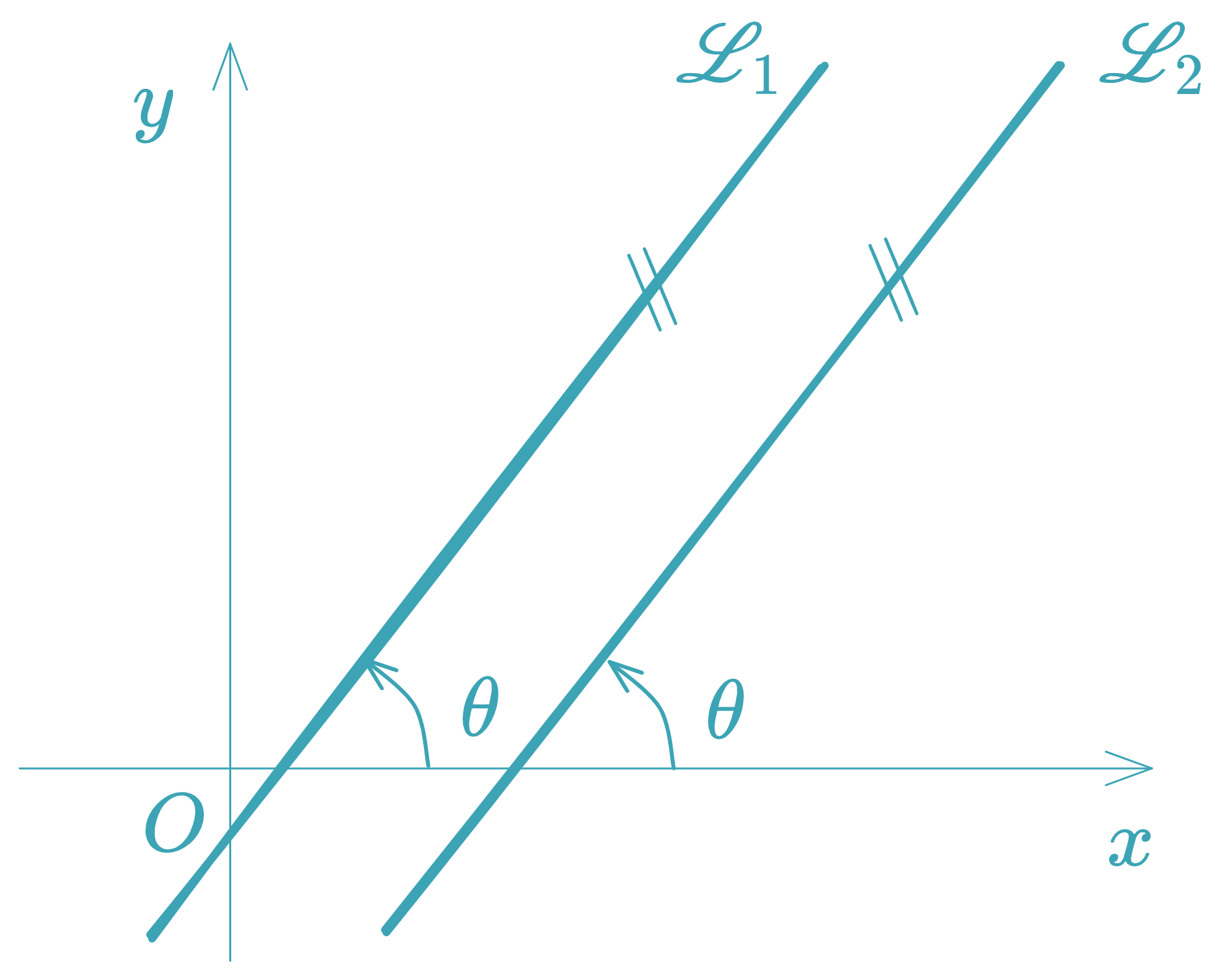
If, in addition, $\dfrac{C_1}{C_2} = \dfrac{A_1}{A_2}$, then the lines are **coincident**.

---

Coincident Lines

Two lines are coincident if all their coefficients are proportional:

$$\boxed{\frac{A_1}{A_2} = \frac{B_1}{B_2} = \frac{C_1}{C_2}}$$

---

Oblique (Intersecting) Lines

Two lines intersect at exactly one point if they are not parallel:

$$\boxed{A_1 B_2 - A_2 B_1 \ne 0}$$

---

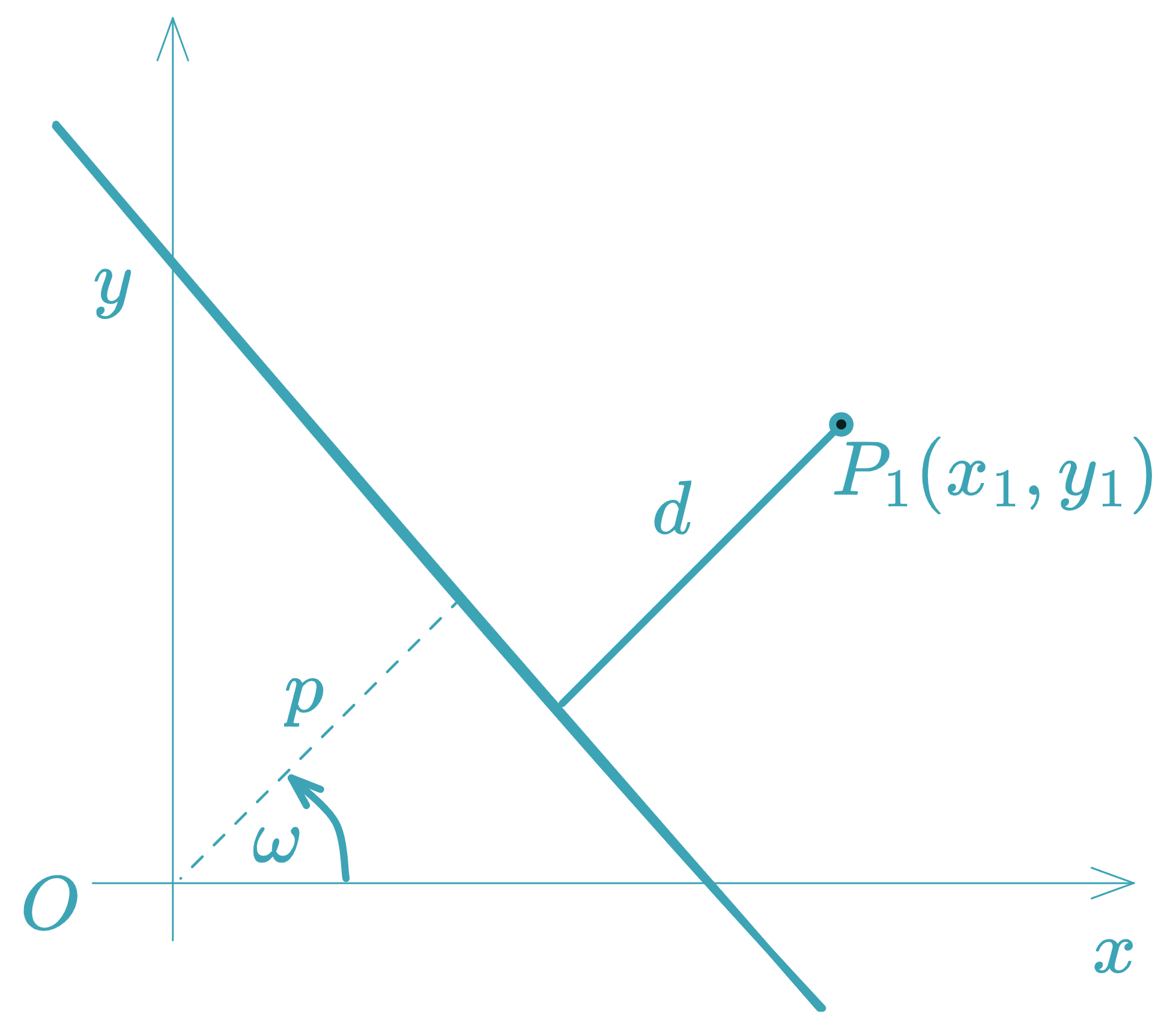
Normal Form of the Equation of a Line

The normal form of a line is:

$$x \cos \omega + y \sin \omega - p = 0$$

Where:

• $\omega$: angle between the normal vector and the positive $x$-axis ($0^\circ \leq \omega < 360^\circ$)
• $p$: perpendicular distance from the origin to the line (always $p \geq 0$)

---

Converting General Form to Normal Form

Given $Ax + By + C = 0$, divide by $\sqrt{A^2 + B^2}$, choosing the sign opposite to that of $C$ to ensure $p \geq 0$:

$$\frac{A}{\pm \sqrt{A^2 + B^2}}x + \frac{B}{\pm \sqrt{A^2 + B^2}}y + \frac{C}{\pm \sqrt{A^2 + B^2}} = 0$$

The sign is chosen so that $\dfrac{C}{\pm \sqrt{A^2 + B^2}} \leq 0$, which guarantees $p = -\dfrac{C}{\pm \sqrt{A^2 + B^2}} \geq 0$.

---

Applications of the Normal Form

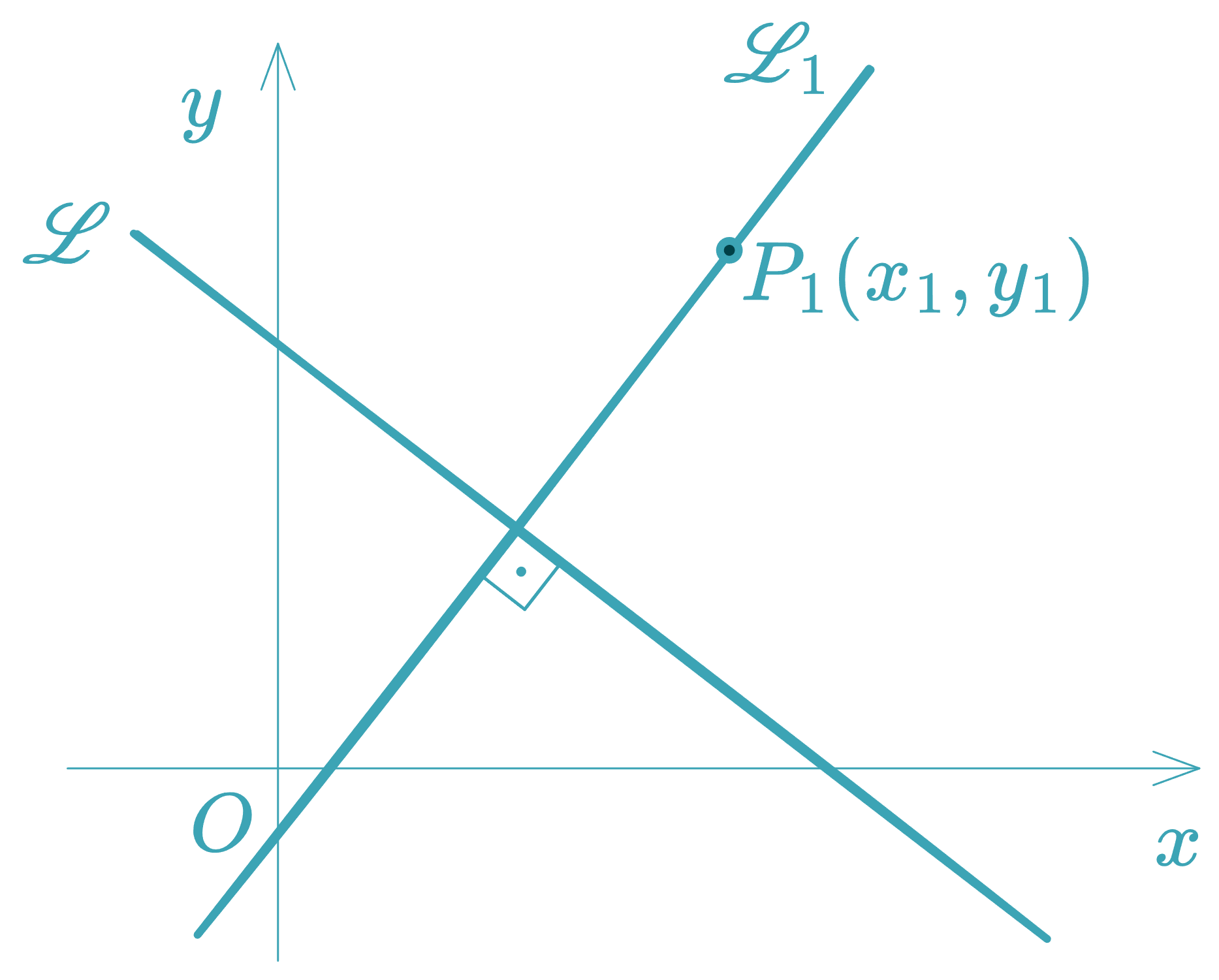
Distance from a Point to a Line (Absolute Distance)

Given a point $P_1(x_1, y_1)$ and a line $Ax + By + C = 0$, the (always non-negative) perpendicular distance is:

$$d(P_1, \mathscr{L}) = \frac{|Ax_1 + By_1 + C|}{\sqrt{A^2 + B^2}}$$

---

Directed Distance from a Point to a Line

The directed distance $d$ carries a sign that depends on the orientation of the normal vector $(A, B)$:

$$d = \frac{Ax_1 + By_1 + C}{\sqrt{A^2 + B^2}}$$

title: Important  
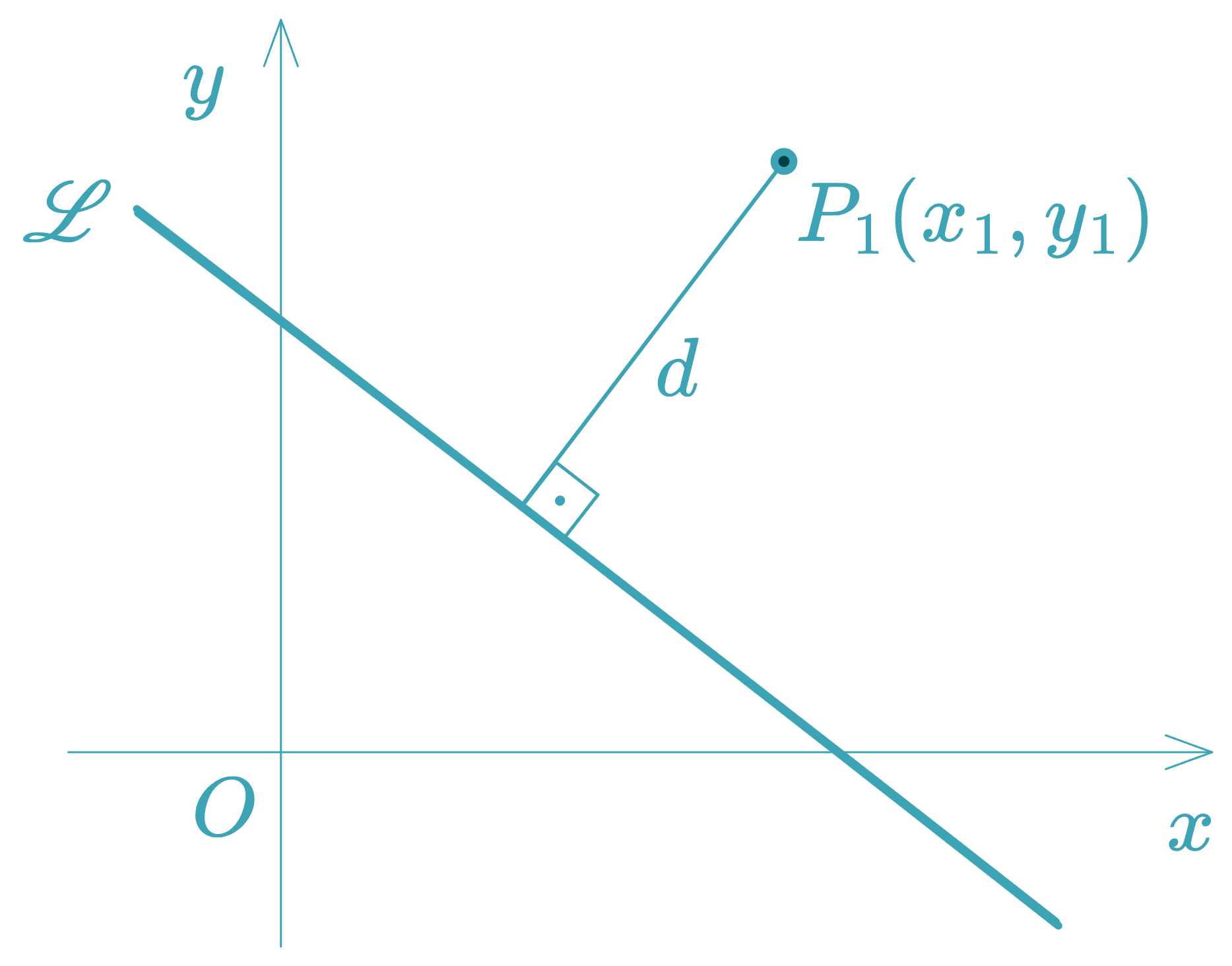
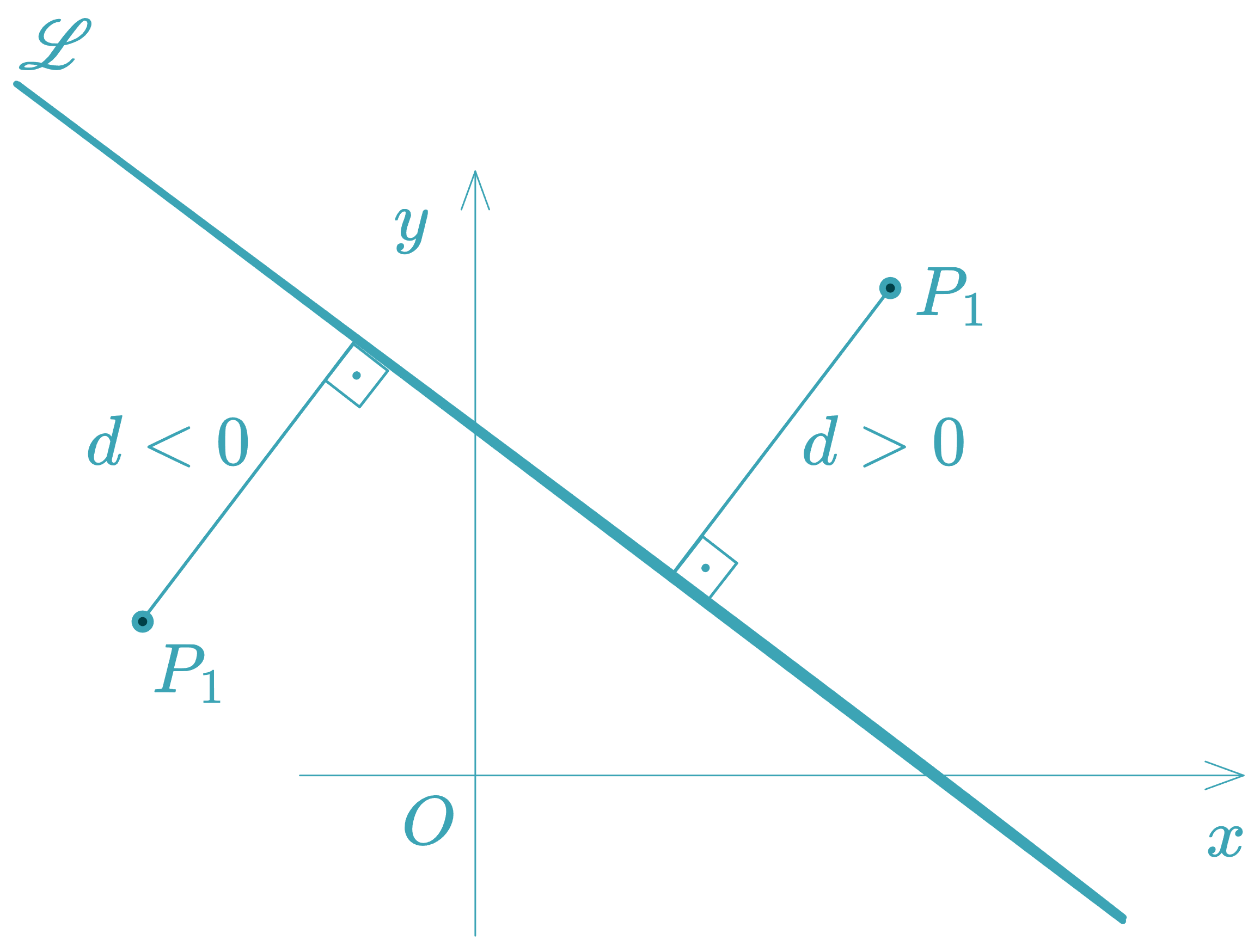
The denominator is always positive. The sign of $d$ depends on the numerator and reflects the point’s position relative to the **normal vector** $(A, B)$:
- If $d > 0$: the point lies in the direction of the normal vector.
- If $d < 0$: the point lies in the opposite direction.

Special Cases:

1. Line not passing through the origin ($C \ne 0$):

   • $d > 0$ if $P_1$ and the origin lie on opposite sides of the line.
   • $d < 0$ if they lie on the same side.

   

2. Line passing through the origin ($C = 0$):

   • $d > 0$ if $P_1$ is "above" the line (in the direction of $(A, B)$).
   • $d < 0$ if it is "below".

   

title: Note:  
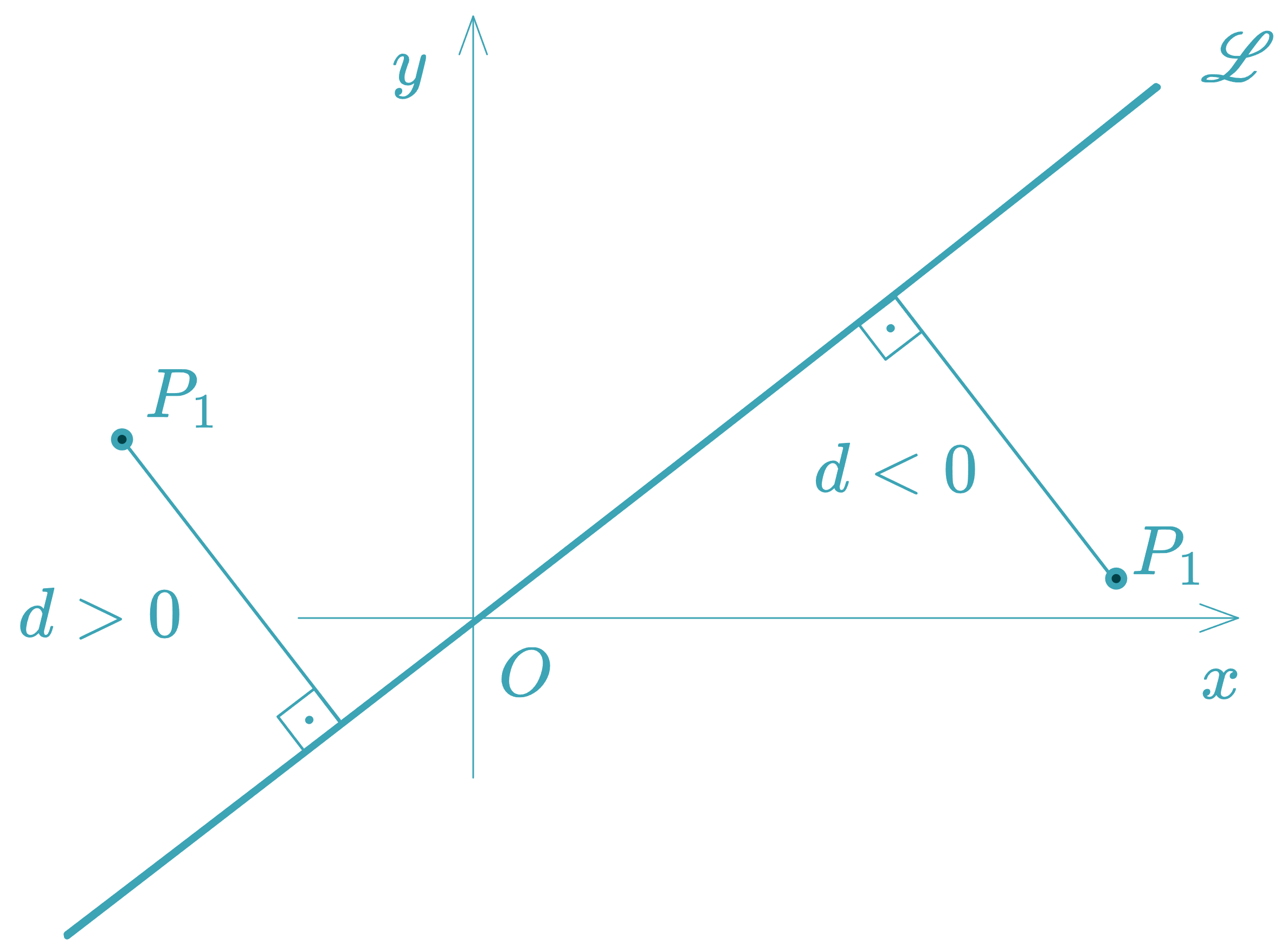
The sign of the directed distance is determined **only by the numerator**. Do **not** include $\pm$ in the denominator—modern convention fixes the denominator as **positive**.

---

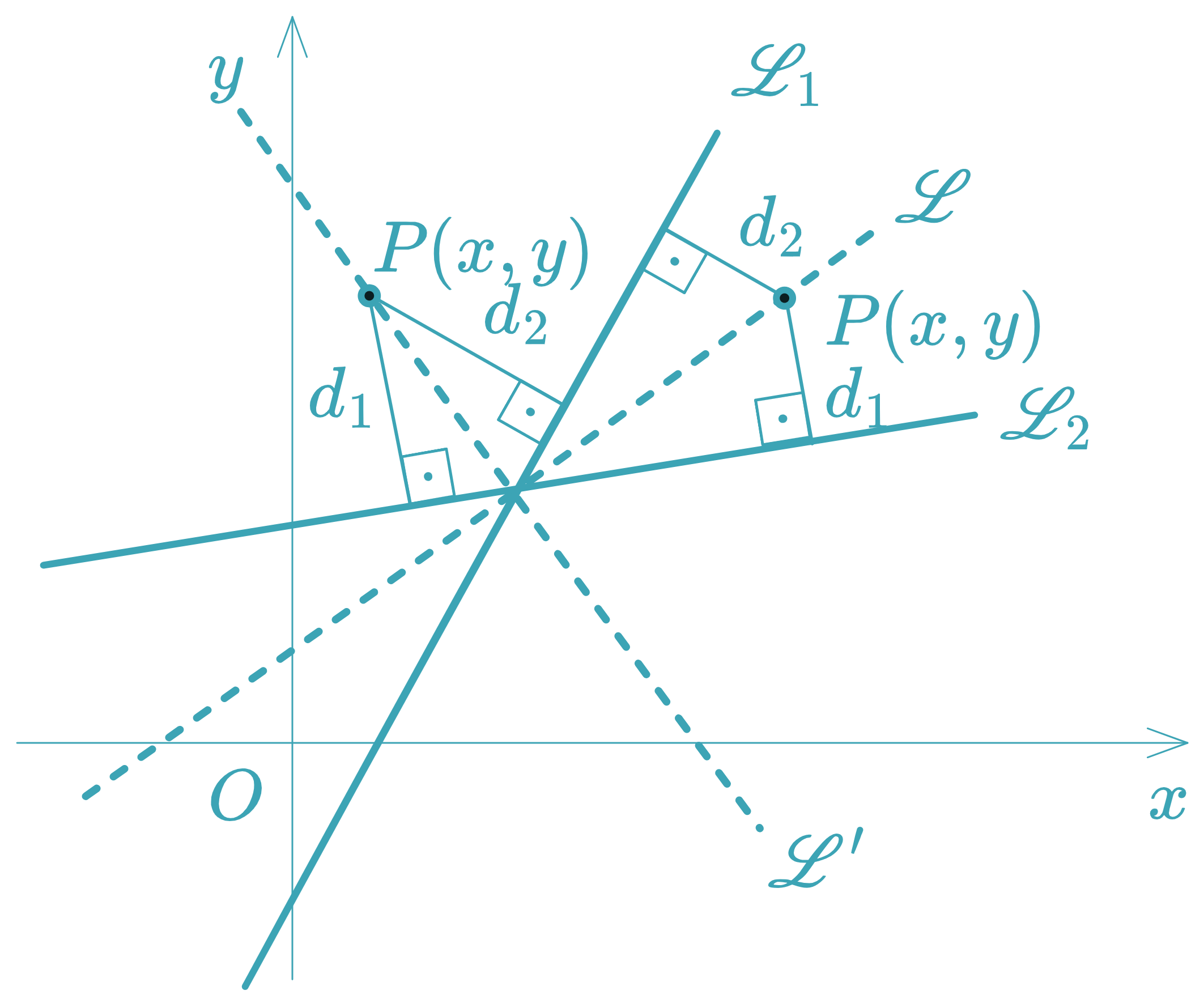
Angle Bisectors of Two Intersecting Lines

Given two lines $\mathscr{L}_1: A_1x + B_1y + C_1 = 0$ and $\mathscr{L}_2: A_2x + B_2y + C_2 = 0$, the angle bisectors are the loci of points equidistant to both lines:

$$\frac{|A_1x + B_1y + C_1|}{\sqrt{A_1^2 + B_1^2}} = \frac{|A_2x + B_2y + C_2|}{\sqrt{A_2^2 + B_2^2}}$$

Removing absolute values gives the two bisectors:

$$\frac{A_1x + B_1y + C_1}{\sqrt{A_1^2 + B_1^2}} = \pm \frac{A_2x + B_2y + C_2}{\sqrt{A_2^2 + B_2^2}}$$

- Use **+** for the bisector of the angle containing the direction of the sum of unit normals (often the **acute** angle).  
- Use **–** for the **obtuse** angle bisector.

---

Distance Between Two Parallel Lines

Given two parallel lines $\mathscr{L}_1: Ax + By + C_1 = 0$ and $\mathscr{L}_2: Ax + By + C_2 = 0$ (same $A$ and $B$), the distance between them is:

$$d = \frac{|C_1 - C_2|}{\sqrt{A^2 + B^2}}$$

title: Note:  
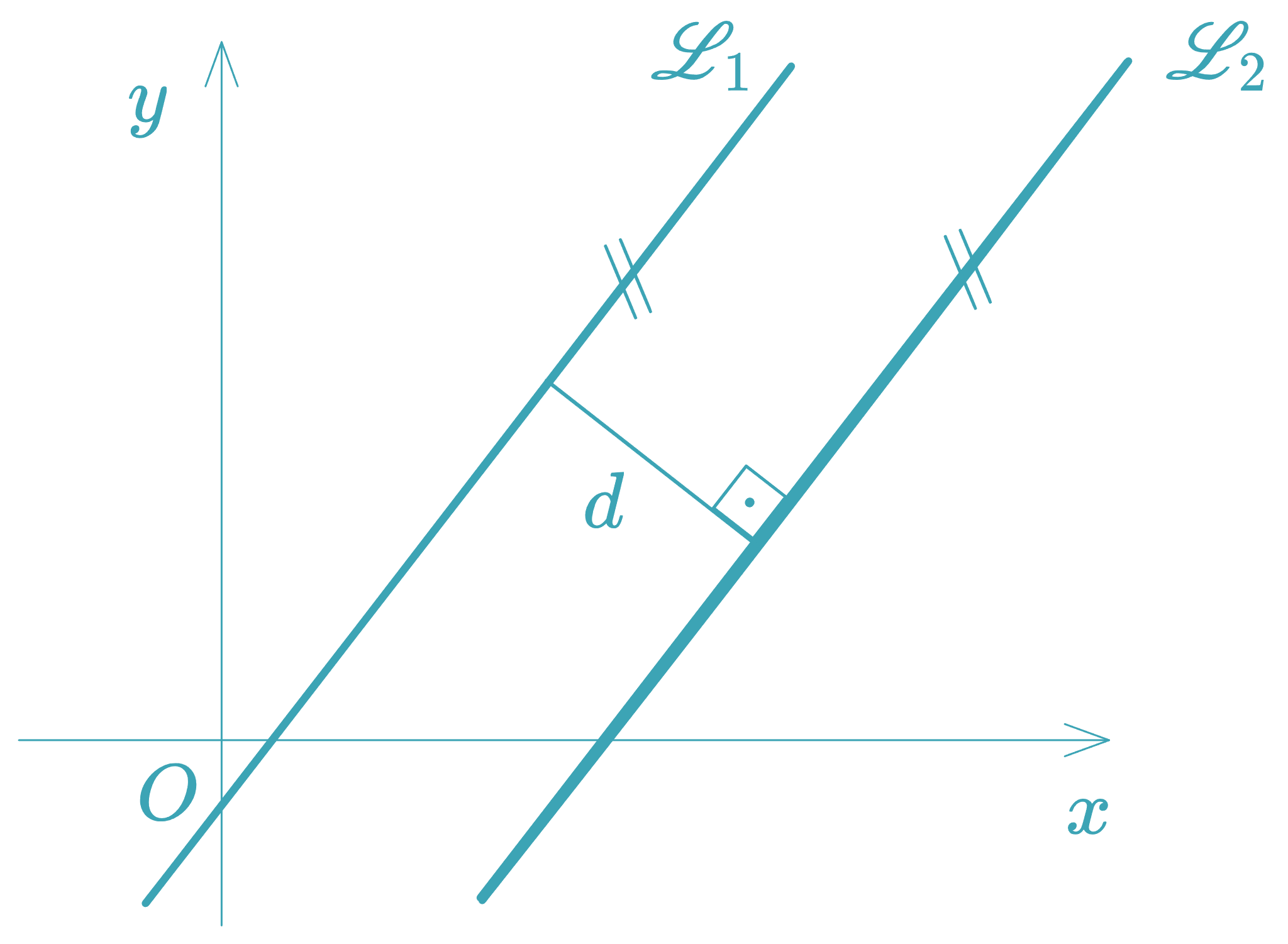
The formulas assume both equations use **identical coefficients** $A$ and $B$.

---

Area of a Triangle

Given three vertices $P_1(x_1, y_1)$, $P_2(x_2, y_2)$, $P_3(x_3, y_3)$, the area of the triangle is:

$$\text{Area} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|$$

Or using a determinant:

$$\text{Area} = \frac{1}{2} \left| \begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \\ \end{vmatrix} \right|$$

---

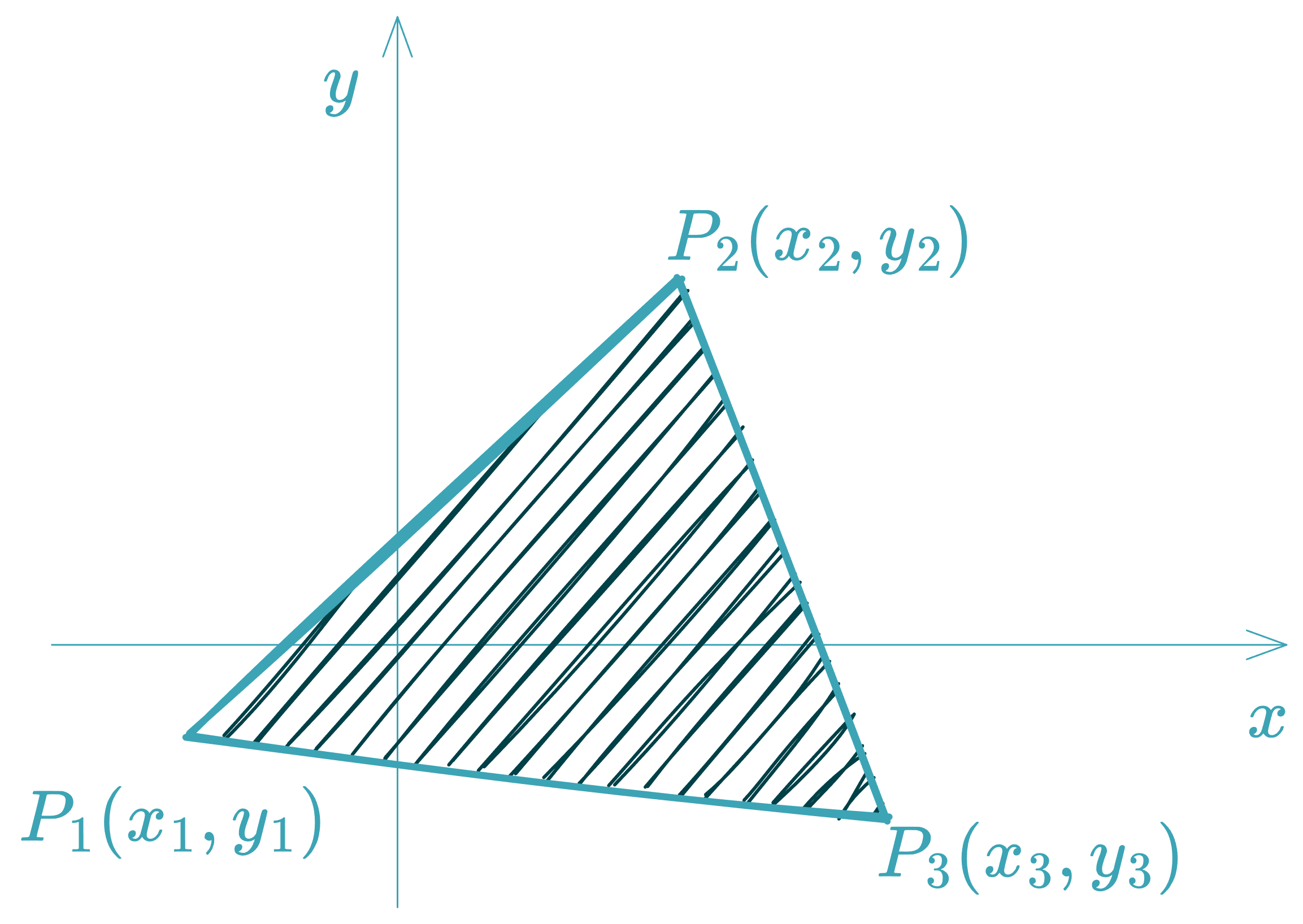
Determinant Form of the Line Through Two Points

Given $P_1(x_1, y_1)$ and $P_2(x_2, y_2)$, the equation of the line is:

$$\begin{vmatrix} x & y & 1 \\ x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ \end{vmatrix} = 0$$

---

Families of Lines

Family of Lines Parallel to a Given Line

Given $Ax + By + C = 0$, the family of parallel lines is:

$$Ax + By + k = 0 \quad \text{for } k \in \mathbb{R}$$

---

Family of Lines Perpendicular to a Given Line

If a given line has slope $m$, all perpendicular lines have slope $-\dfrac{1}{m}$. If they pass through a fixed point $(x_0, y_0)$:

$$y - y_0 = -\frac{1}{m}(x - x_0)$$

In general form: if the original line is $Ax + By + C = 0$, then all perpendicular lines have the form $Bx - Ay + k = 0$.

---

Family of Lines Concurrent at a Point

Given two intersecting lines $\mathscr{L}_1: A_1x + B_1y + C_1 = 0$ and $\mathscr{L}_2: A_2x + B_2y + C_2 = 0$, the family of all lines passing through their intersection point is:

$$A_1x + B_1y + C_1 + \lambda(A_2x + B_2y + C_2) = 0 \quad \text{for } \lambda \in \mathbb{R}$$

title: Note:  
The value $\lambda = -1$ may correspond to a line at infinity or a degenerate case, depending on the context.

Practice Problems

Level I

Level II

Level III