The Circle

Definition

A circle is the locus of all points in the plane that are equidistant from a fixed point called the center. The constant distance from the center to any point on the circle is called the radius.

---

Elements of the Circle

![Elements of the Circle](https://res.cloudinary.com/dze1acg2c/image/upload/v1766501620/equationzone/sa9eg8jjqzul5sszd3co.png)
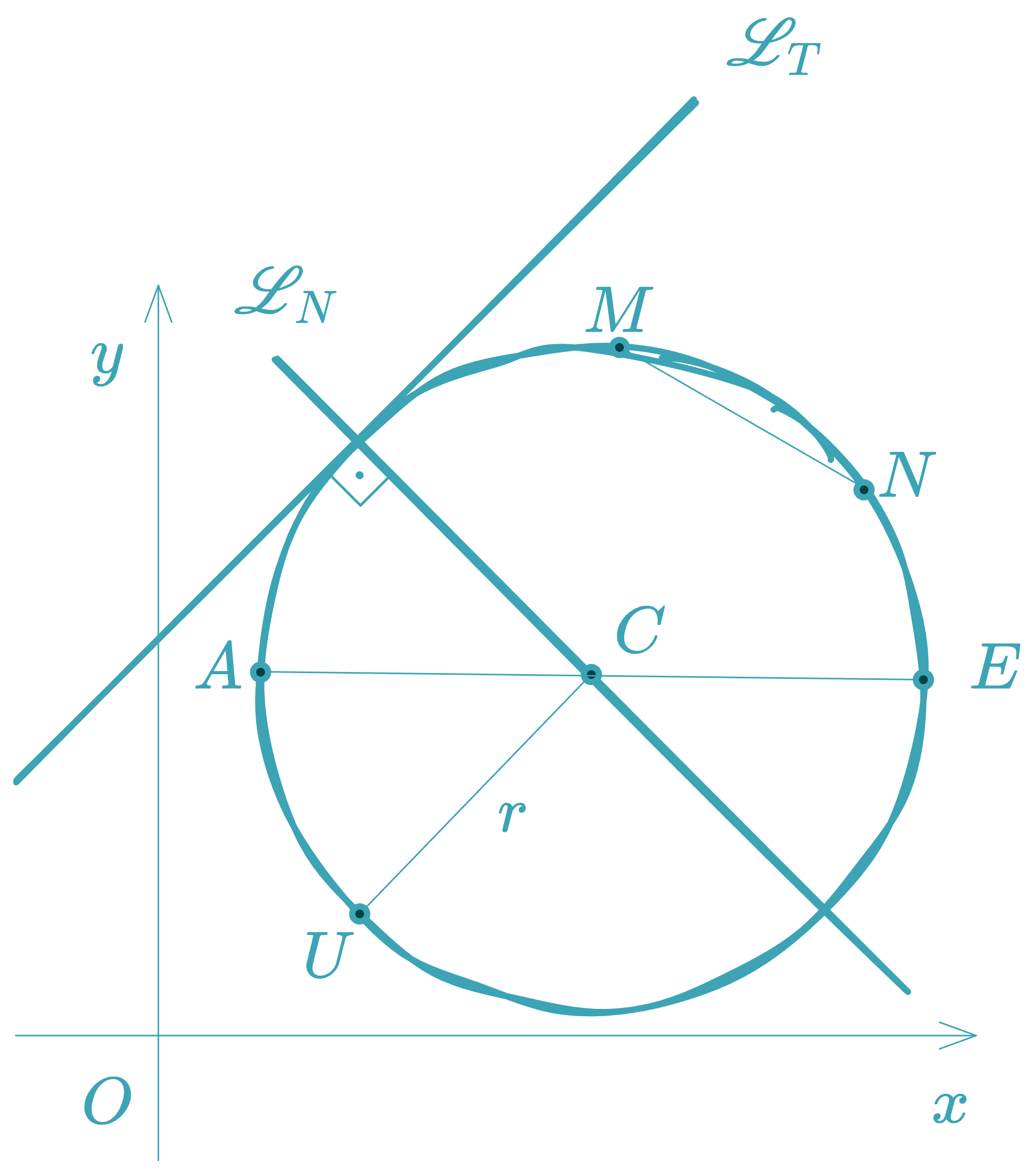
- **Center** ($C$): The fixed interior point from which all points on the circle are equidistant.
- **Radius** ($r = CU$): The distance from the center to any point on the circle.
- **Diameter** ($d$): A chord passing through the center. It satisfies $d = 2r$.
- **Chord** ($\overline{MN}$): A segment joining any two points on the circle.
- **Arc**: A portion of the circumference between two points.
- **Tangent**: A line that intersects the circle at **exactly one point**.
- **Secant**: A line that intersects the circle at **two distinct points**.

---

Equations of the Circle

1. Standard Form (Center at $(h, k)$)

$$\boxed{\mathscr{C}:(x - h)^2 + (y - k)^2 = r^2}$$

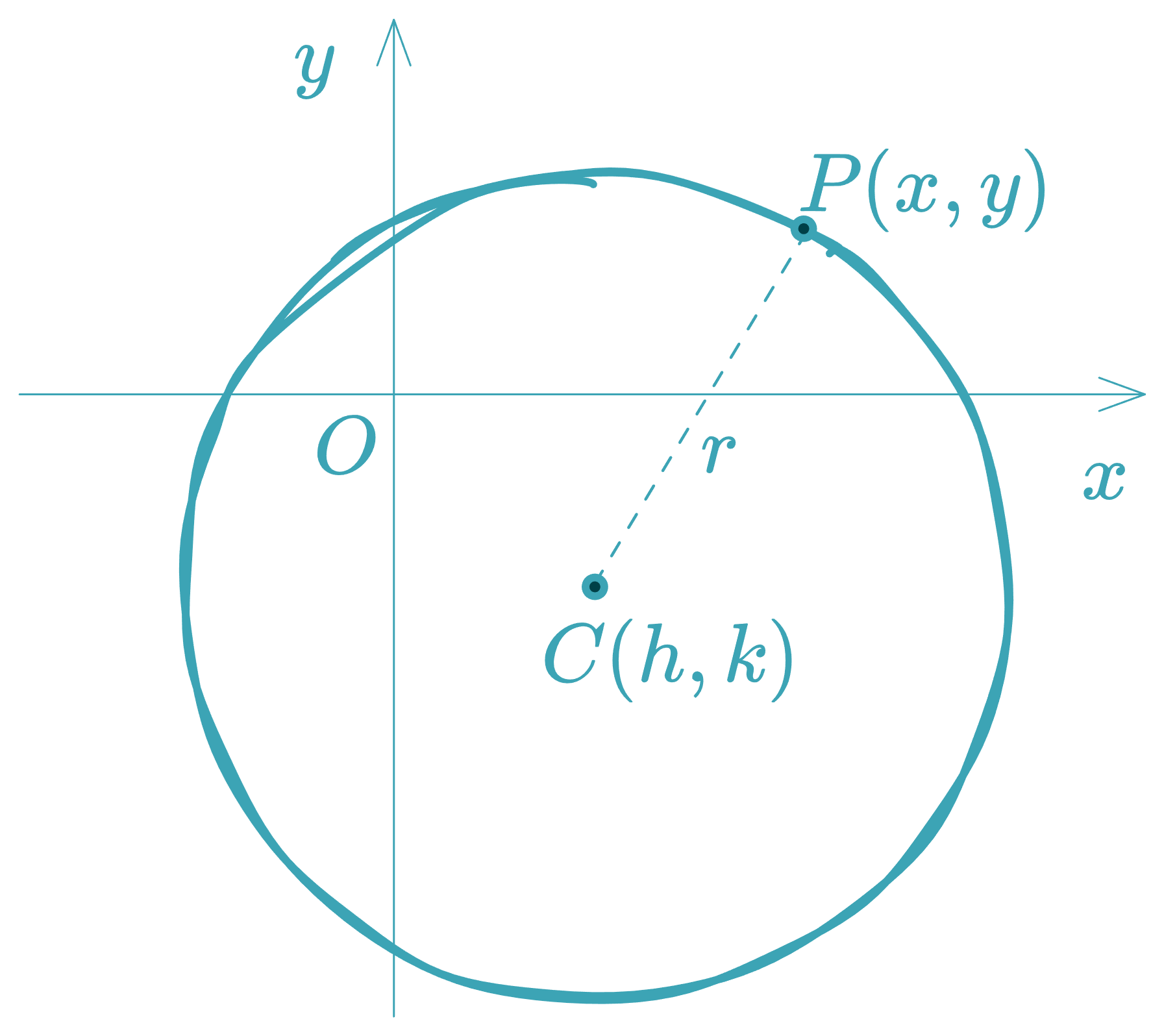
This is the equation of a circle with center $(h, k)$ and radius $r > 0$.

---

2. Canonical Form (Center at the Origin)

$$\boxed{\mathscr{C}: x^2 + y^2 = r^2}$$

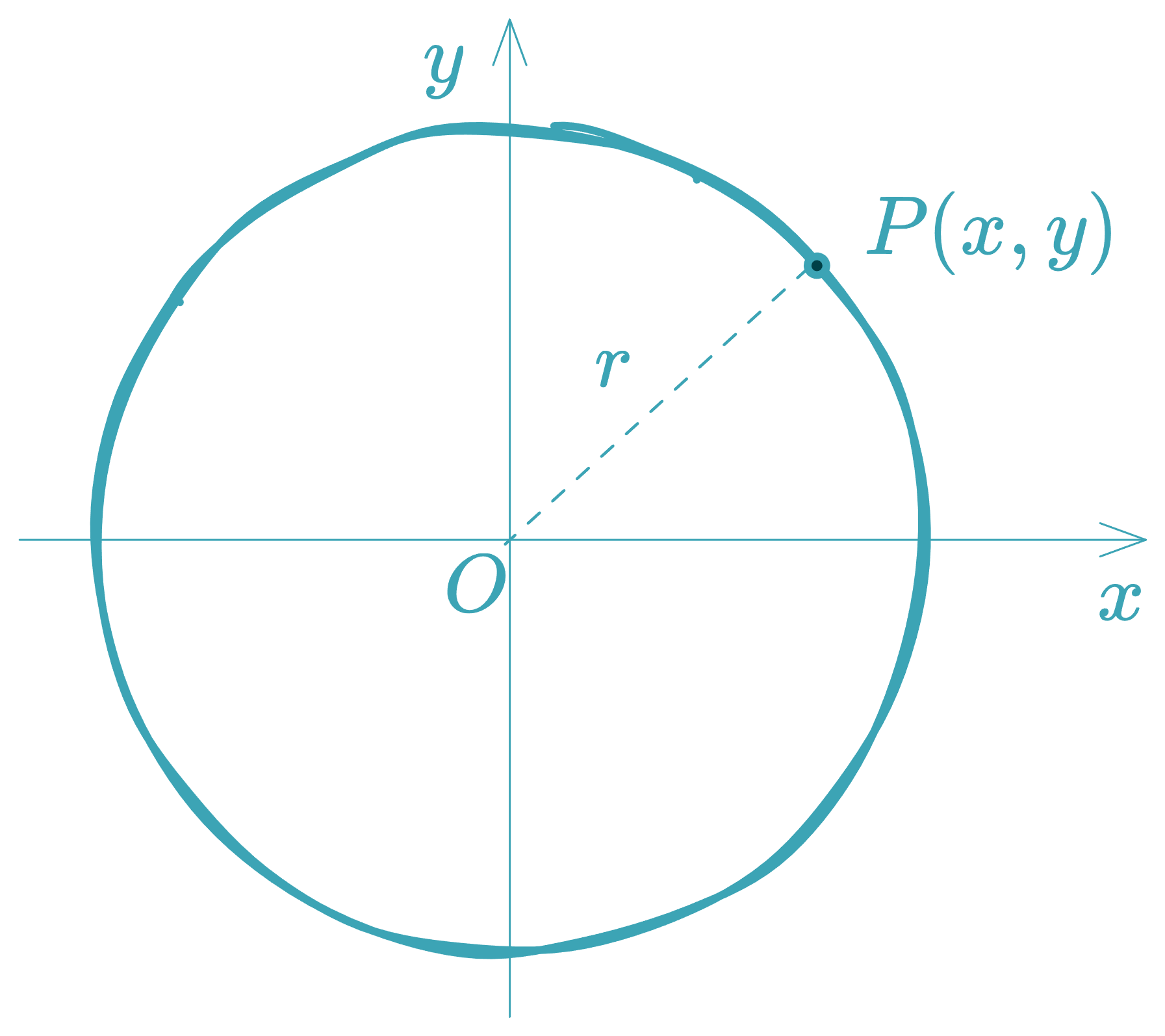
Special cases:

• If $r = 1$: $x^2 + y^2 = 1$ → the unit circle.
• If $r = 0$: $x^2 + y^2 = 0$ → represents only the point $(0, 0)$.

Circle Tangent to the Coordinate Axes

• Tangent to the $x$-axis:
  Center at $(h, k)$, radius $r = |k|$ →

  $$(x - h)^2 + (y - k)^2 = k^2$$

  

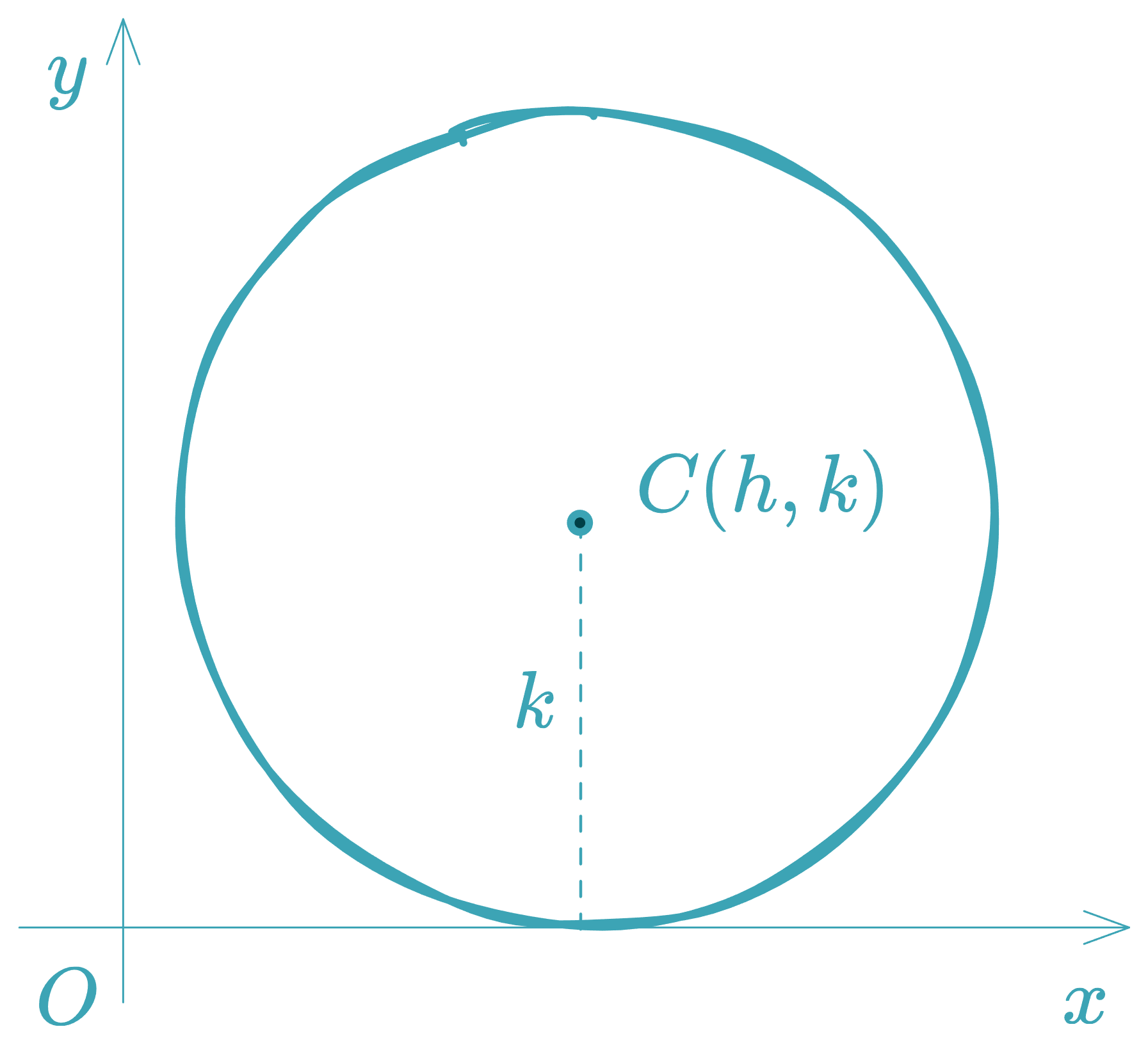
• Tangent to the $y$-axis:
  Center at $(h, k)$, radius $r = |h|$ →

  $$(x - h)^2 + (y - k)^2 = h^2$$

  

---

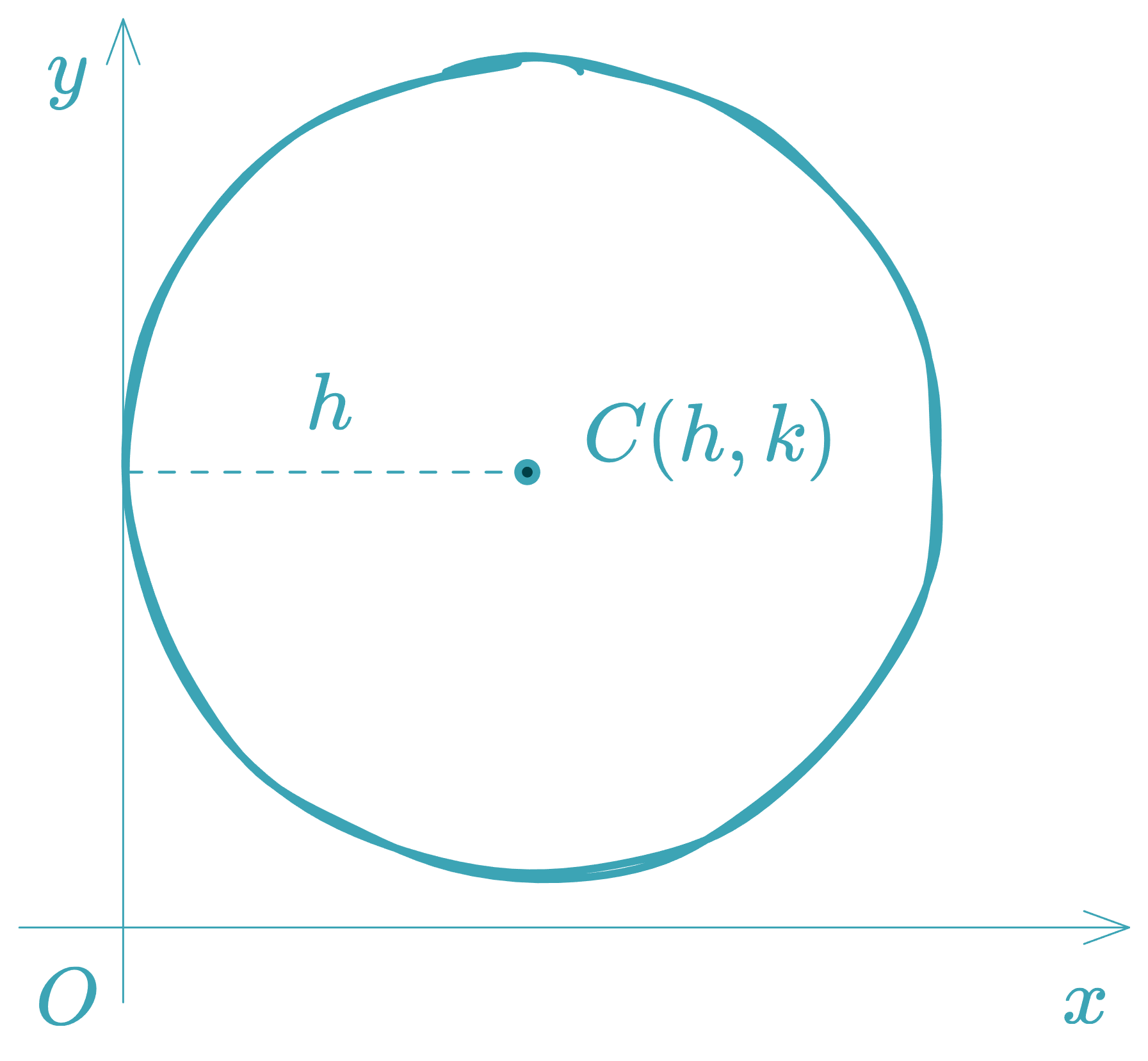
3. Parametric Equations

Given center $C = (x_0, y_0)$ and radius $r$, any point $M$ on the circle can be expressed as:

$$\begin{cases} x = x_0 + r \cos \theta \\ y = y_0 + r \sin \theta \end{cases} \quad \text{with } \theta \in [0, 2\pi)$$

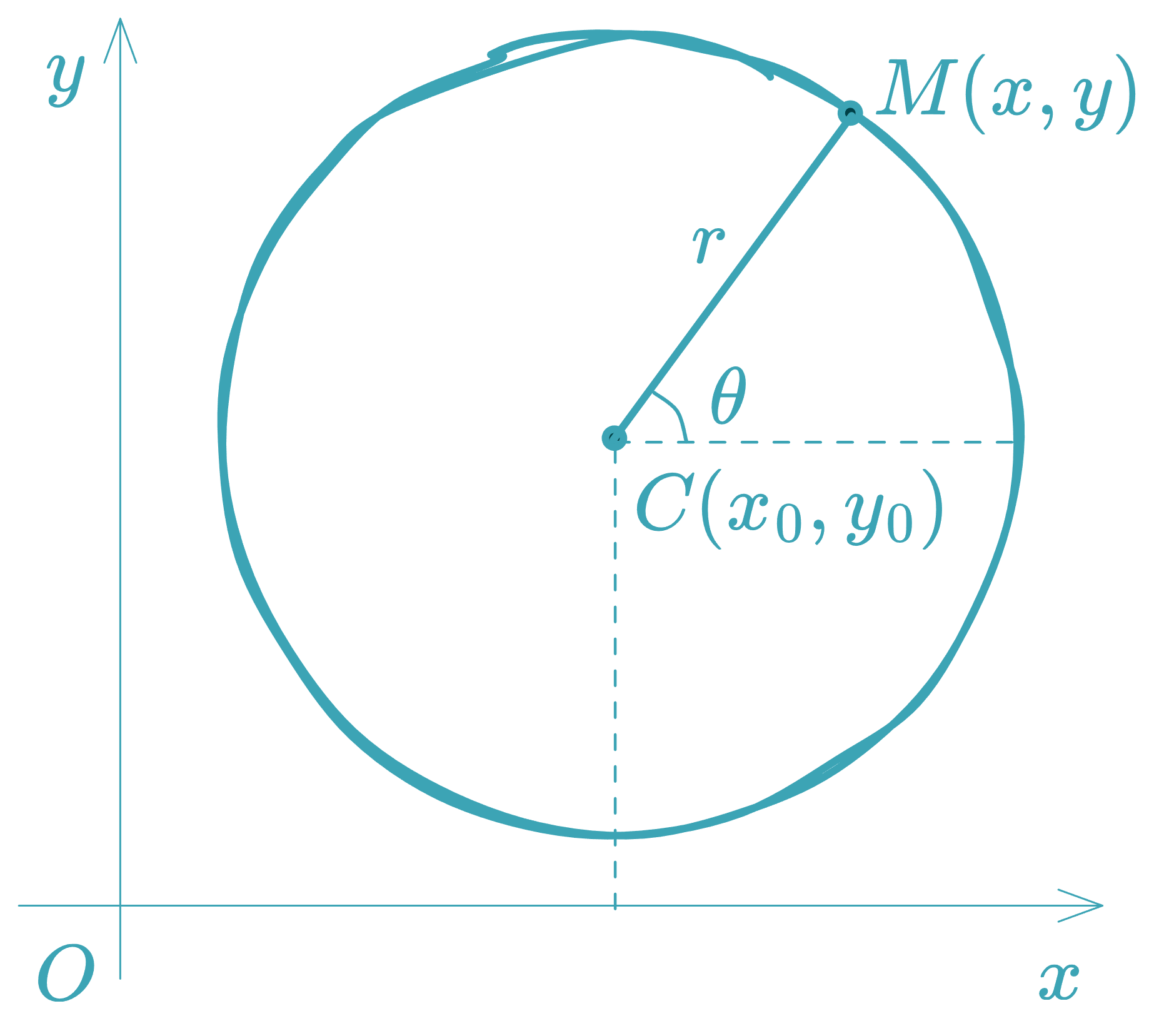
where $\theta$ is the angle measured from the positive $x$-axis.

---

4. Polar Equation

• General circle (center at $(\rho_0, \varphi_0)$, radius $r$):

$$\rho^2 - 2\rho\rho_0\cos(\varphi - \varphi_0) + \rho_0^2 = r^2$$

title: Note:
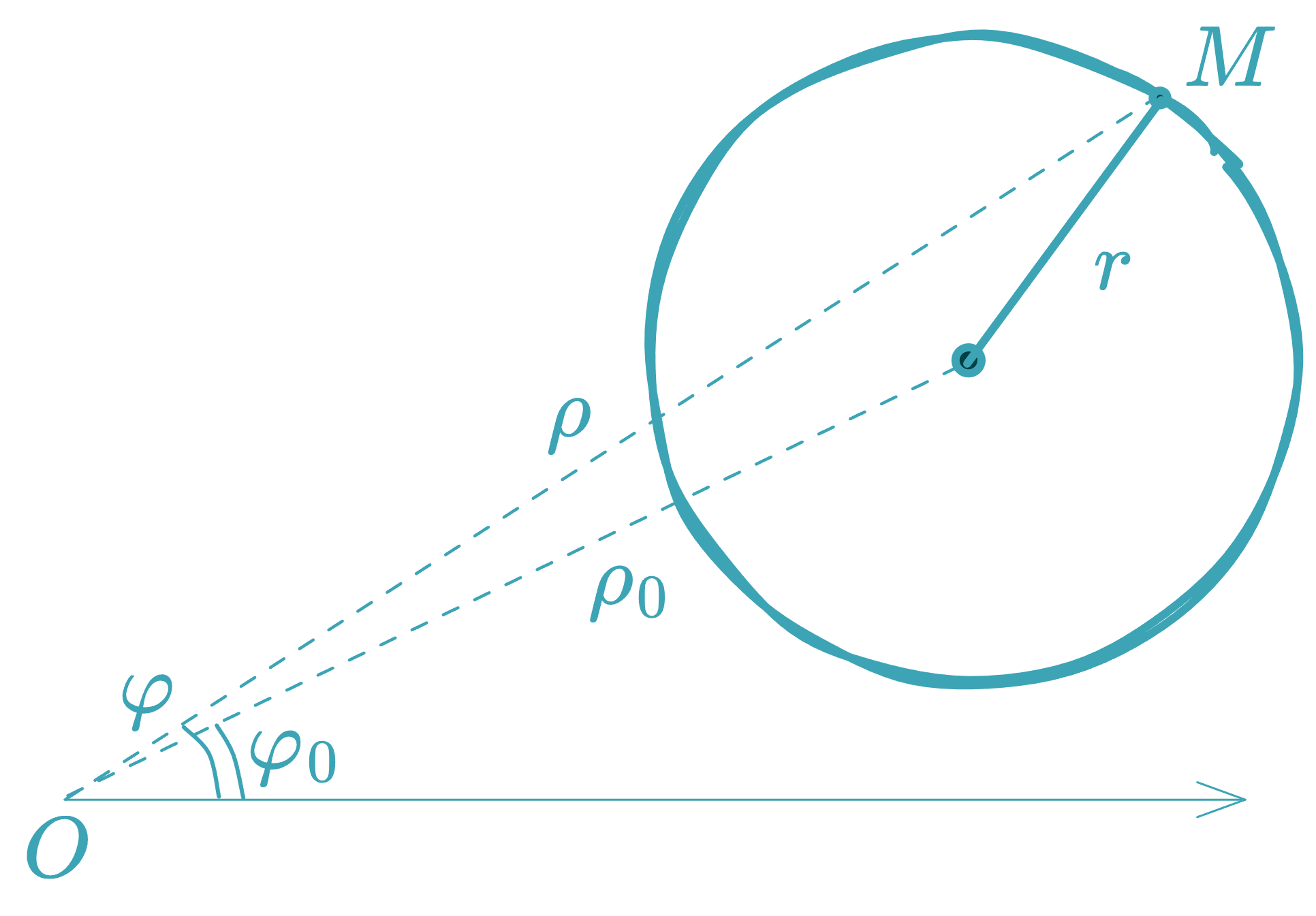
Some texts use a plus sign, but the above form aligns with the Law of Cosines and is preferred for consistency.

• Special case: Circle passing through the pole with center on the polar axis ($\varphi = 0$):

$$\boxed{\rho = 2r \cos \varphi}$$

---

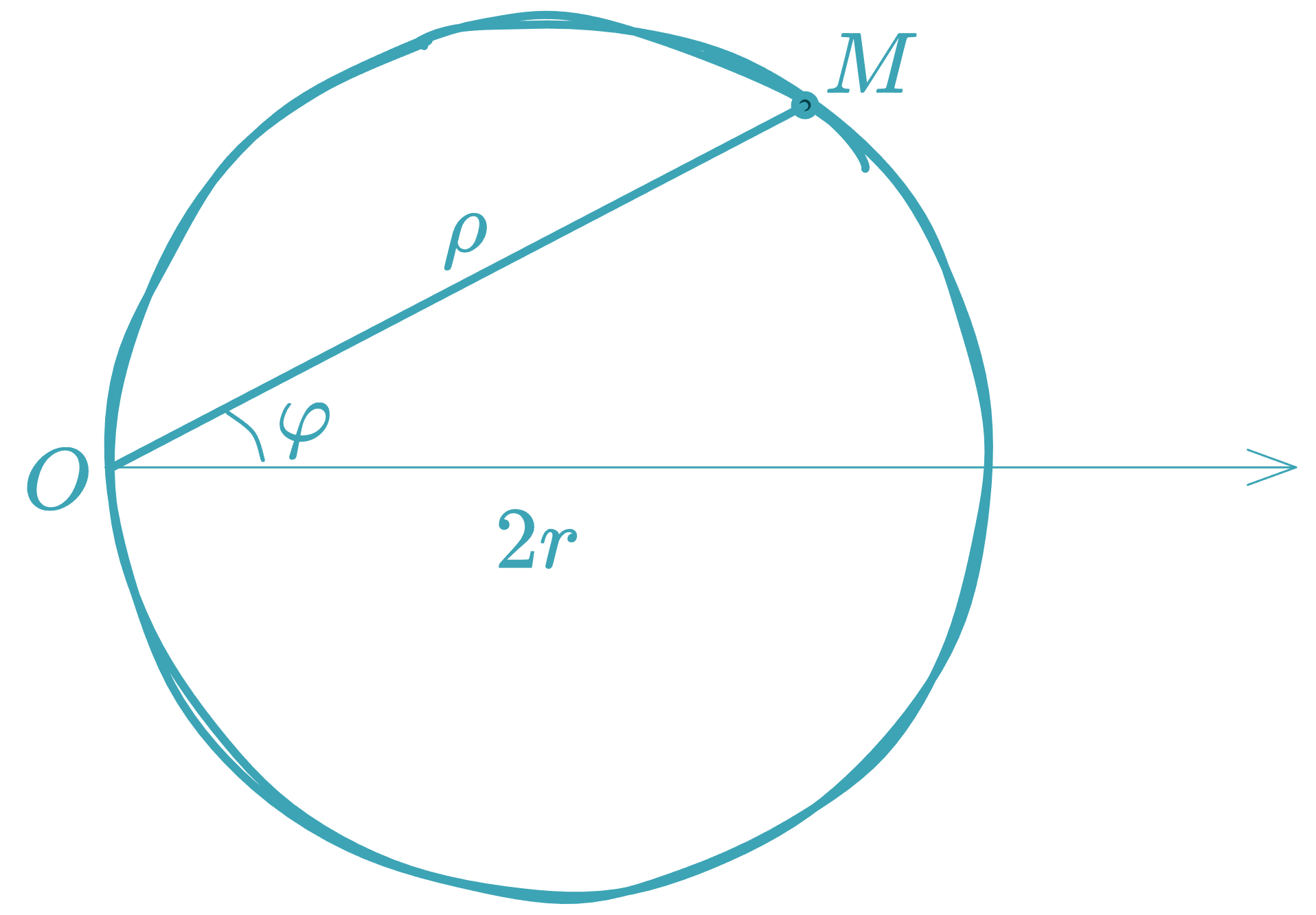
5. General Form of the Equation

$$\boxed{x^2 + y^2 + Dx + Ey + F = 0}$$

• Center: $\left(-\dfrac{D}{2},\ -\dfrac{E}{2}\right)$
• Radius: $r = \sqrt{\left(\dfrac{D}{2}\right)^2 + \left(\dfrac{E}{2}\right)^2 - F}$

title: Condition for a real circle
$$\left(\dfrac{D}{2}\right)^2 + \left(\dfrac{E}{2}\right)^2 - F > 0$$
- If the expression equals zero, the equation represents a **point circle**.
- If negative, it represents an **imaginary circle** (no real points).

---

Determining a Circle

Three independent conditions are required to uniquely determine a circle. Common cases include:

• Three non-collinear points.
• Center and radius.
• Center and a point on the circle.
• Two points and the tangent line at one of them.
• One point and two tangent lines.

Substitute the given conditions into the standard or general form and solve the resulting system of equations.

---

Families of Circles

Given two circles:

$$\begin{aligned} \mathscr{C}_1 &: x^2 + y^2 + D_1x + E_1y + F_1 = 0 \\ \mathscr{C}_2 &: x^2 + y^2 + D_2x + E_2y + F_2 = 0 \end{aligned}$$

The family of all circles passing through their points of intersection is:

$$\mathscr{C}_1 + \lambda \mathscr{C}_2 = 0 \quad (\lambda \in \mathbb{R},\ \lambda \ne -1)$$

Equivalently:

$$x^2 + y^2 + D_1x + E_1y + F_1 + \lambda(x^2 + y^2 + D_2x + E_2y + F_2) = 0$$

title: Note:
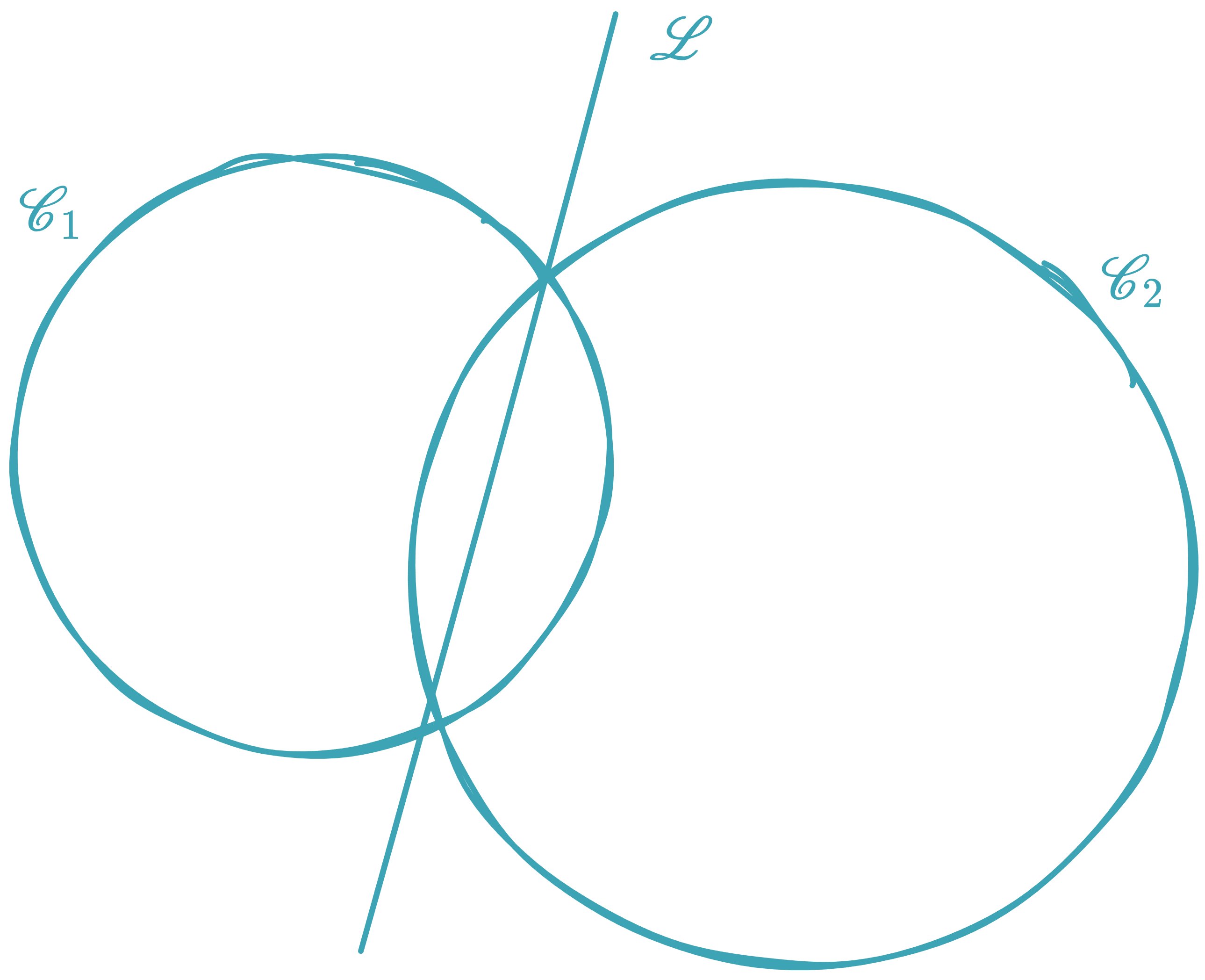
The equation $\mathscr{C}_1 - \mathscr{C}_2 = 0$ yields the **radical axis**—the straight line containing all points with equal power with respect to both circles.

---

Tangent Lines to a Circle

1. Tangent at a Point $P(x_1, y_1)$ on the Circle

• Circle centered at the origin ($x^2 + y^2 = r^2$):

$$x x_1 + y y_1 = r^2$$

• Circle with center $(h, k)$:

$$(x - h)(x_1 - h) + (y - k)(y_1 - k) = r^2$$

2. Tangency Condition for a Line

Given a line $Ax + By + C = 0$ and a circle with center $(h, k)$ and radius $r$, the line is tangent if and only if the perpendicular distance from the center to the line equals the radius:

$$\frac{|Ah + Bk + C|}{\sqrt{A^2 + B^2}} = r$$

---

Coordinate Transformations

1. Translation of Axes

If the coordinate axes are translated so that the new origin is at $(h, k)$, the coordinates relate by:

$$\begin{cases} x = x' + h \\ y = y' + k \end{cases} \quad \text{or inversely} \quad \begin{cases} x' = x - h \\ y' = y - k \end{cases}$$

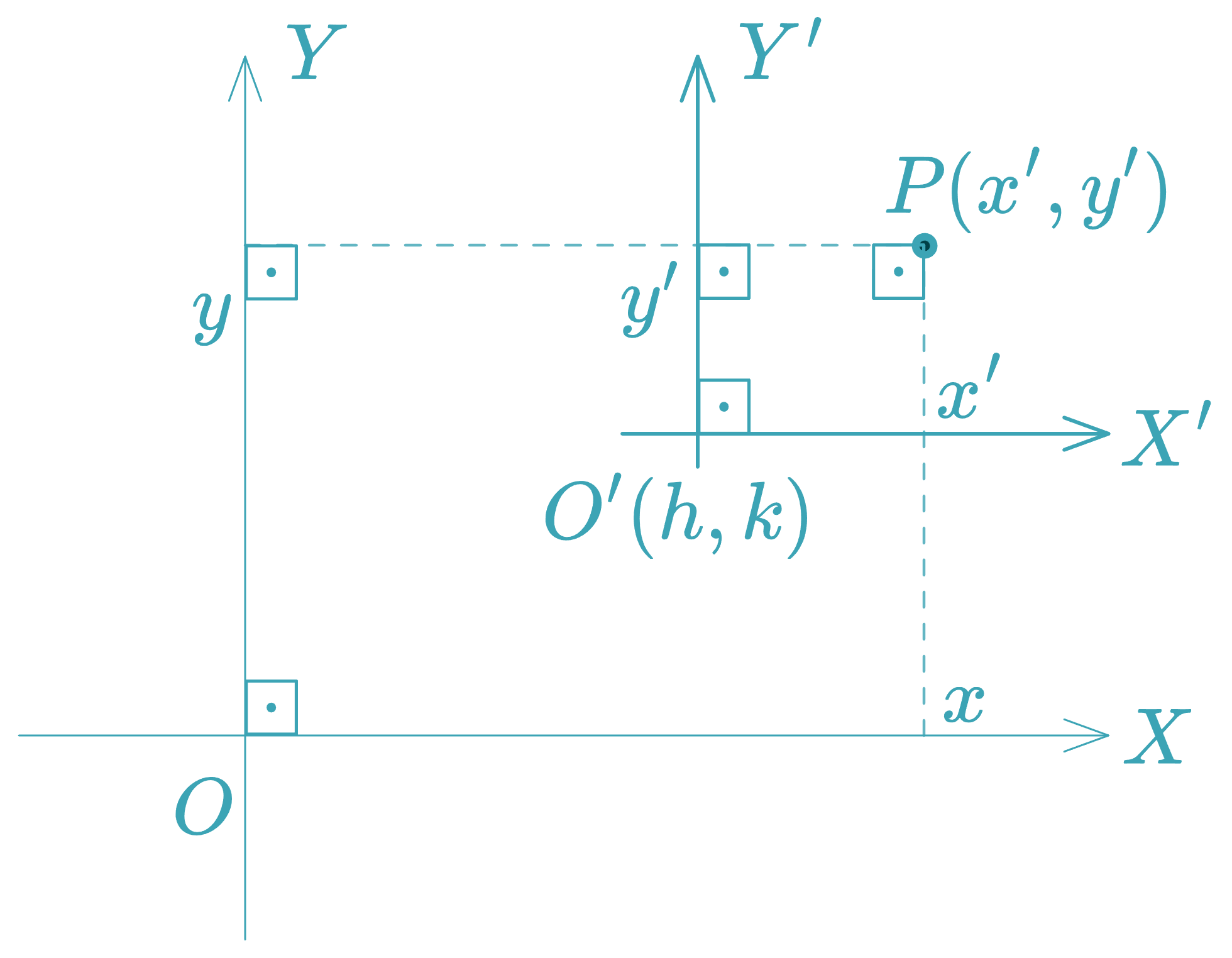
This transformation eliminates linear terms in the general equation, simplifying it to canonical form.

---

2. Rotation of Axes

Rotating the axes by an angle $\theta$ relates original $(x, y)$ and new $(x', y')$ coordinates by:

$$\begin{cases} x = x' \cos\theta - y' \sin\theta \\ y = x' \sin\theta + y' \cos\theta \end{cases}$$

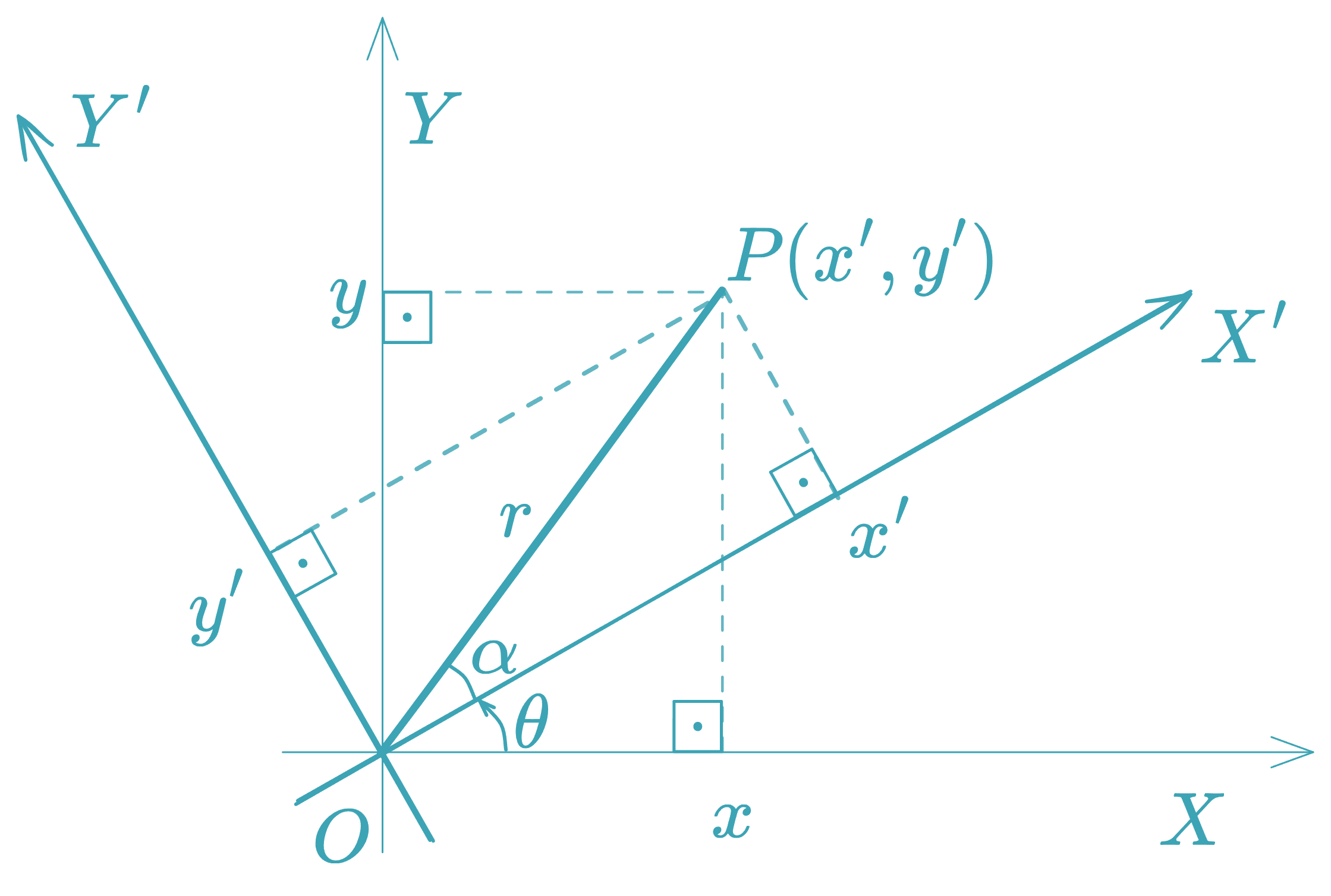
3. Eliminating the $xy$ Term in Conic Sections

For a general quadratic equation

$$Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0,$$

the mixed term $xy$ is eliminated by rotating the axes through an angle $\theta$ satisfying:

$$\tan(2\theta) = \frac{B}{A - C} \quad \text{(if } A \ne C\text{)}$$

If $A = C$, then $\theta = 45^\circ$.

title: Note:
Although the **circle never contains an $xy$ term** (due to its rotational symmetry), this technique is essential for analyzing other conic sections and is included here for completeness in the context of coordinate transformations.

Practice Problems

Level I

Level II

Level III