Plane Figure Areas

Area of Plane Figures

Triangle

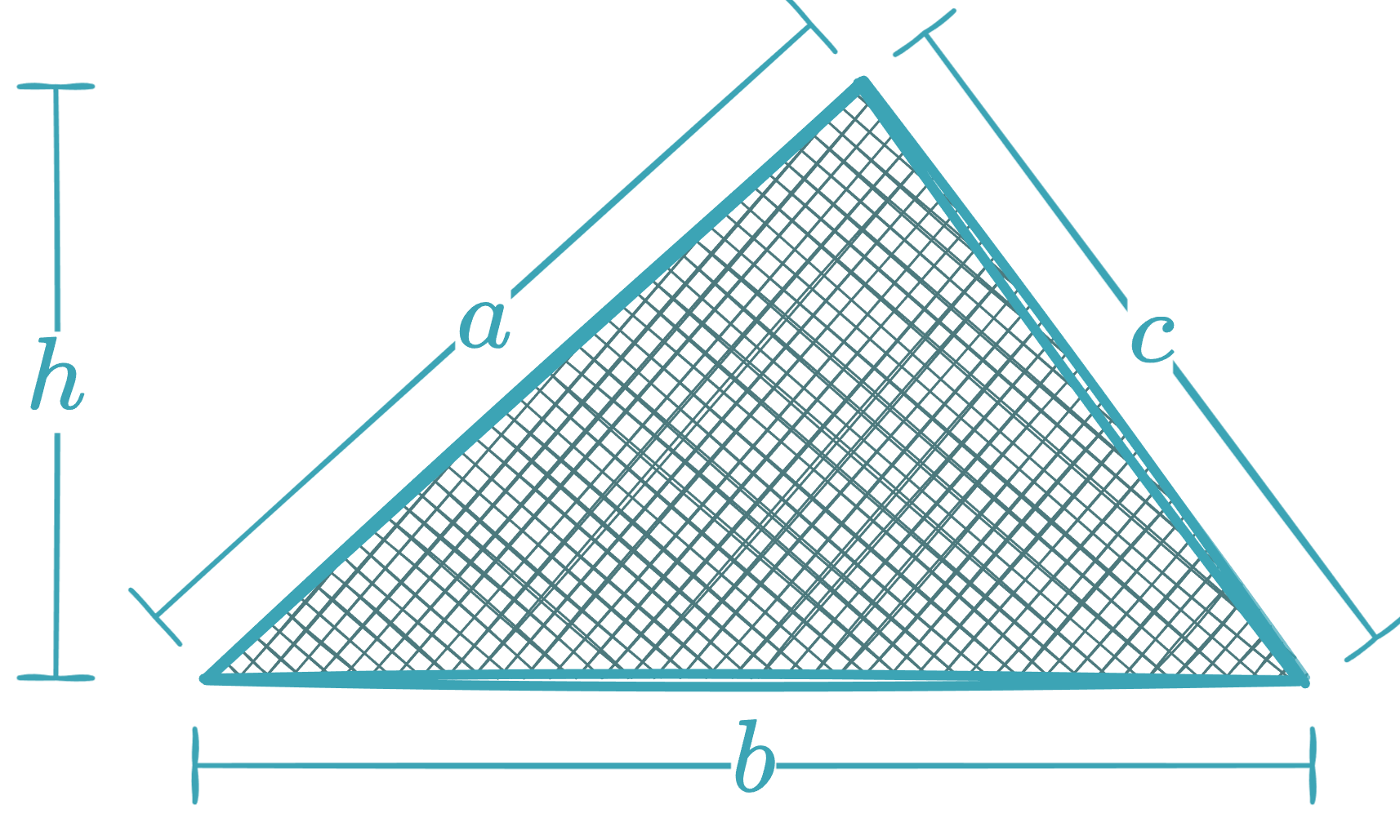
• General formula (base and height):

  $$A = \frac{b \cdot h}{2}$$

• Heron’s Formula (sides):

  $$A = \sqrt{s(s-a)(s-b)(s-c)}$$

  where $s = \frac{a + b + c}{2}$ is the semiperimeter.

Acute Triangle

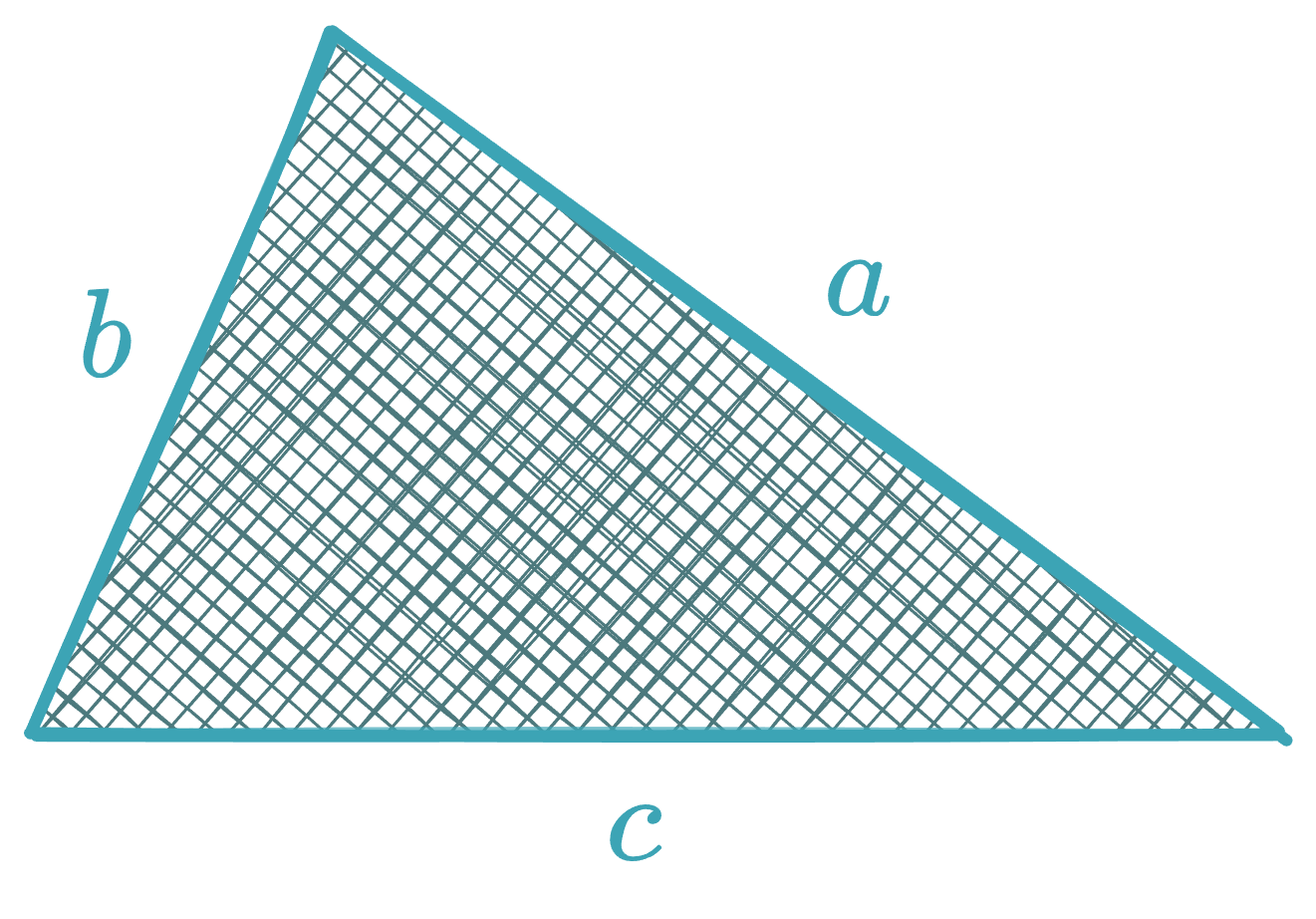
Given two sides ($a$, $b$) and base $c$:

$$A = \frac{c}{2} \sqrt{a^2 - \left( \frac{a^2 - b^2 + c^2}{2c} \right)^2}$$

Obtuse Triangle

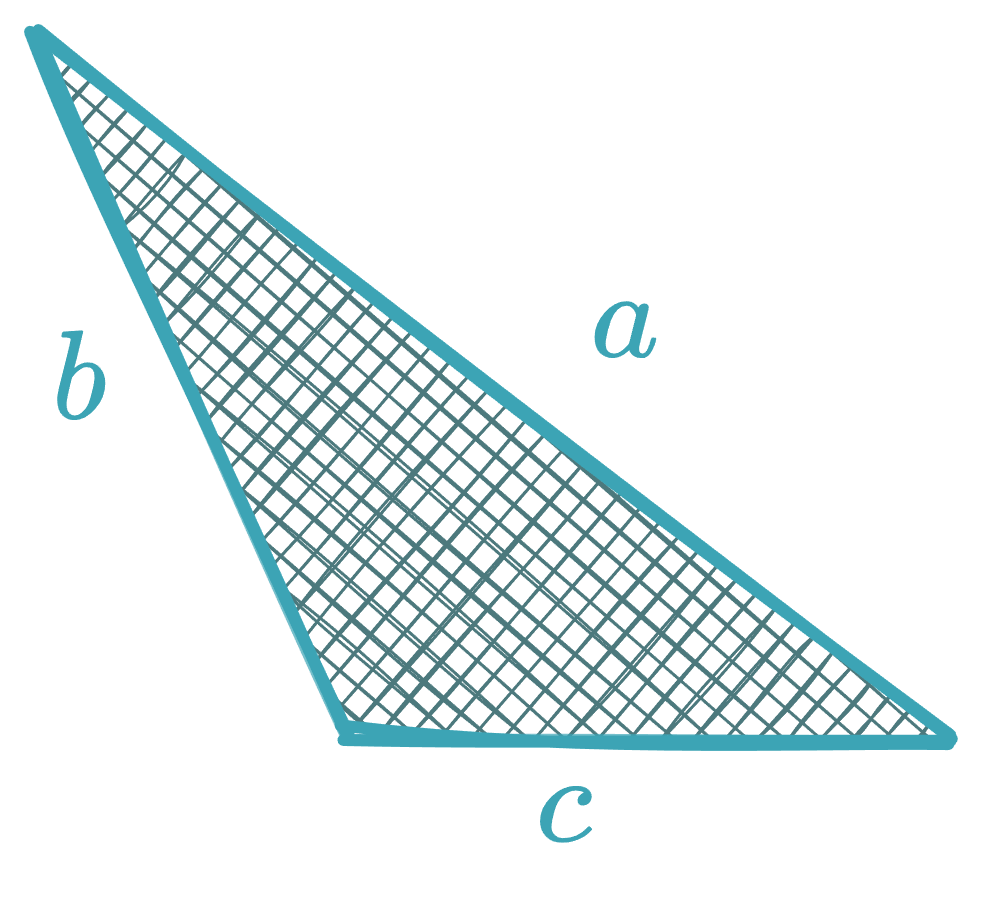
Given two sides ($a$, $b$) and base $c$:

$$A = \frac{c}{2} \sqrt{b^2 - \left( \frac{a^2 - b^2 - c^2}{2c} \right)^2}$$

Equilateral Triangle

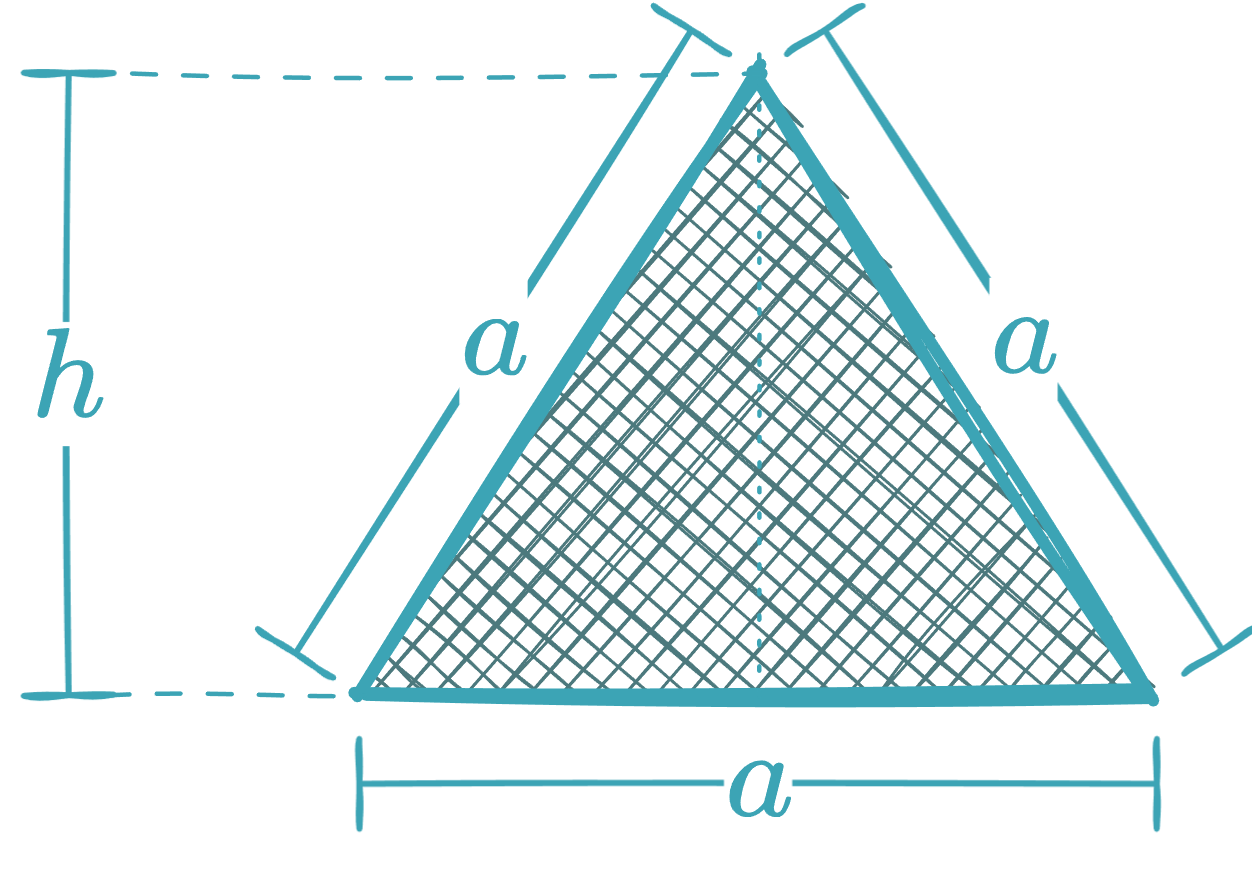
• With side $a$ and height $h$:

  $$A = \frac{a \cdot h}{2}$$

  $$h = \frac{\sqrt{3}}{2} a$$

• In terms of side $a$:

  $$A = \frac{\sqrt{3}}{4} a^2$$

• In terms of height $h$:

  $$A = \frac{\sqrt{3}}{3} h^2$$

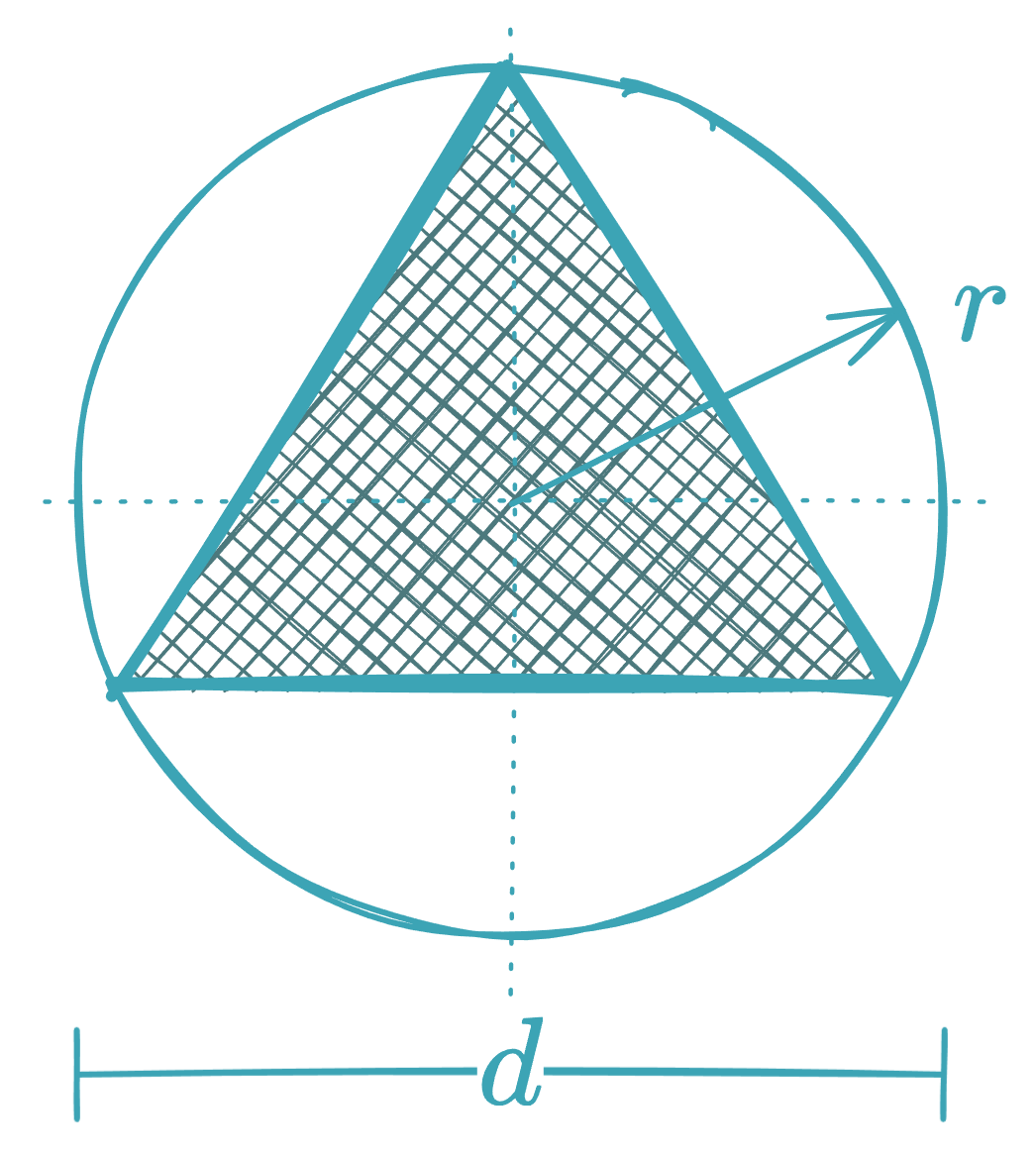
• In terms of the diameter $d$ of the circumscribed circle:

  $$A = \frac{3\sqrt{3}}{16} d^2$$

• In terms of the radius $r$ of the inscribed circle:

  $$A = \frac{3\sqrt{3}}{4} r^2$$

Square

• In terms of side $l$:

  $$A = l^2$$

  $$l = \sqrt{A}$$

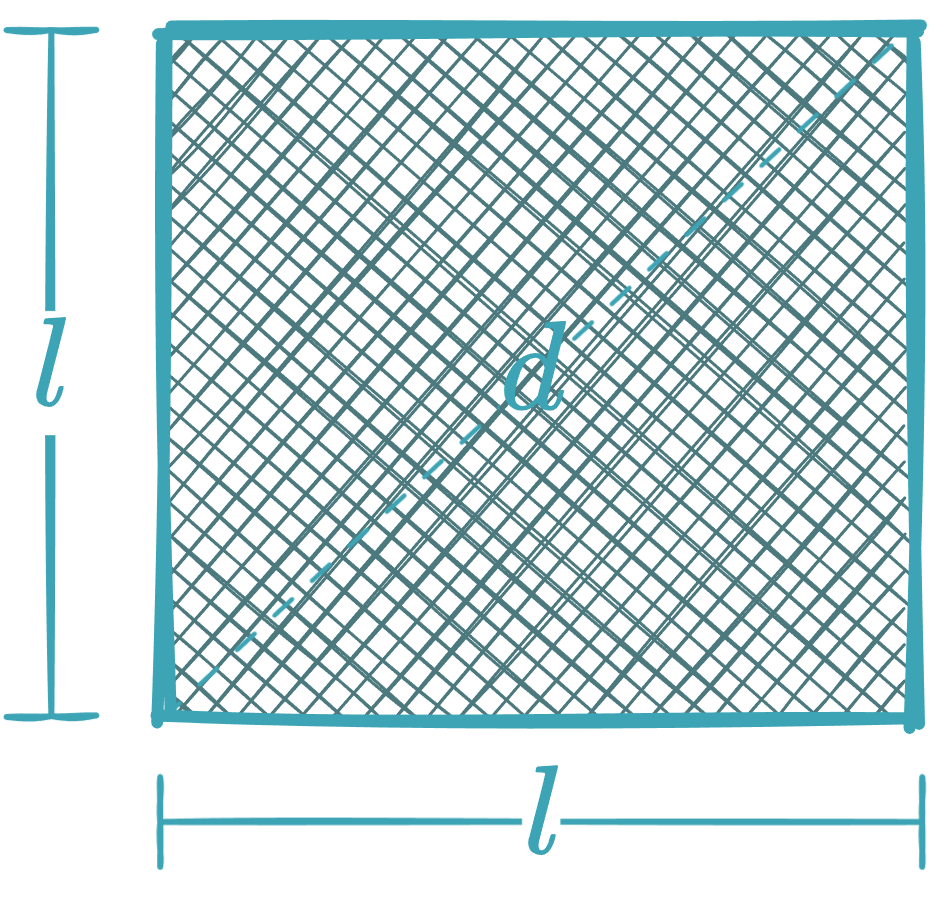
• In terms of diagonal $d$:

  $$d = l \cdot \sqrt{2}$$

  $$A = \frac{d^2}{2}$$

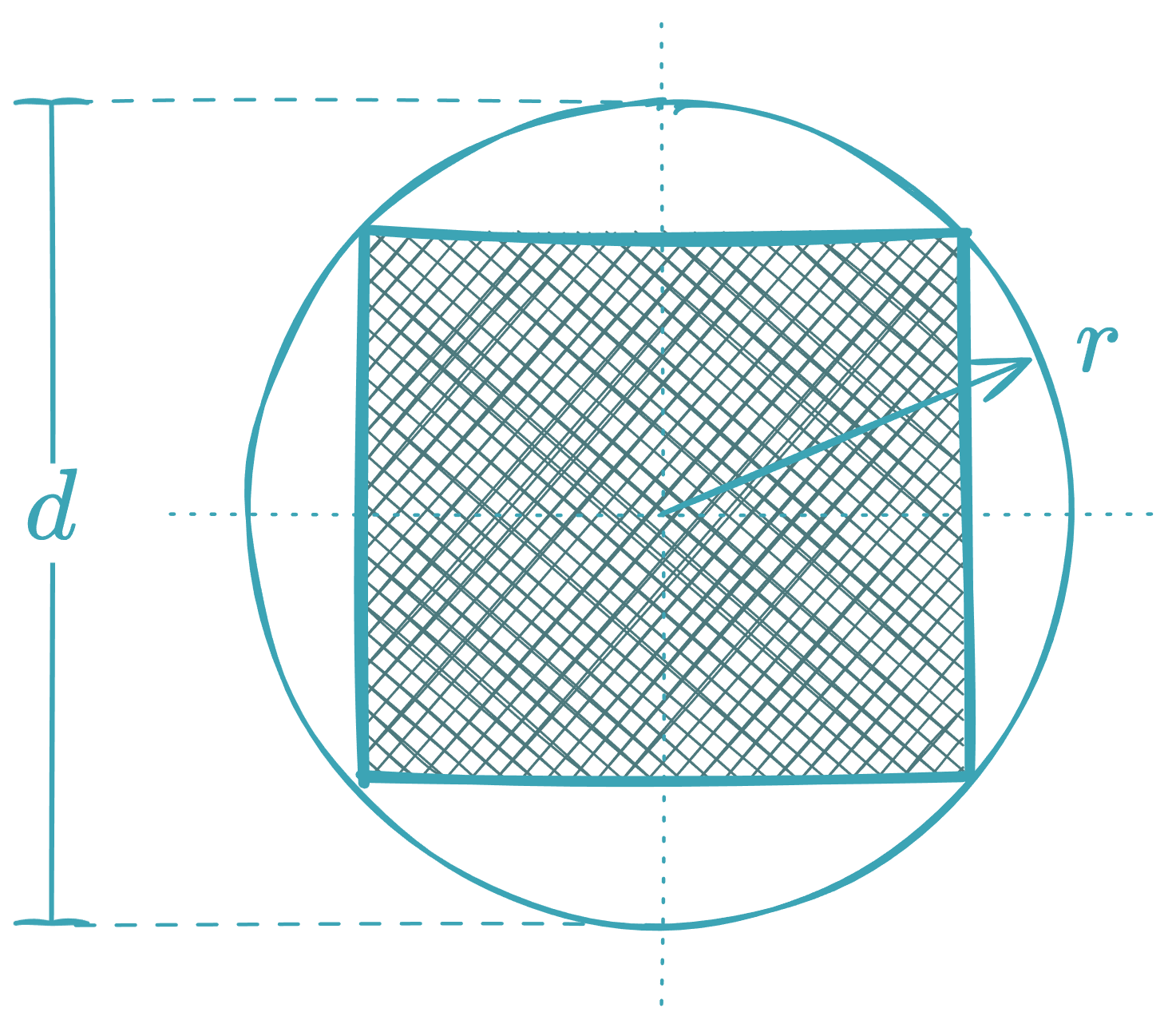
• In terms of the radius $r$ of the inscribed circle:

  $$A = (2r)^2 = 4r^2$$

Rectangle

$$A = b \cdot h$$

$$d = \sqrt{b^2 + h^2}$$

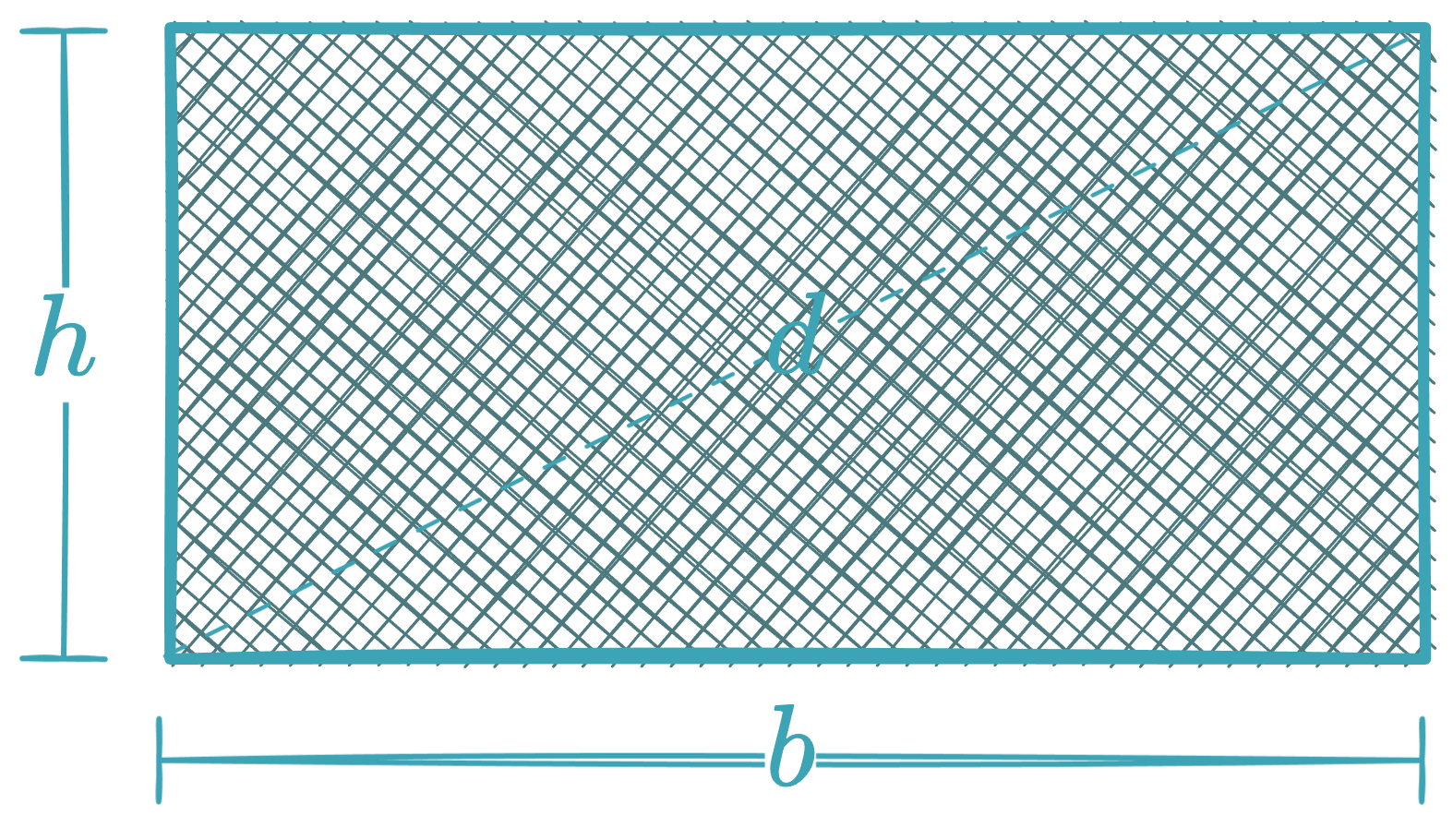
(where $d$ is the diagonal, $b$ the base and $h$ the height)

Parallelogram

• Area:

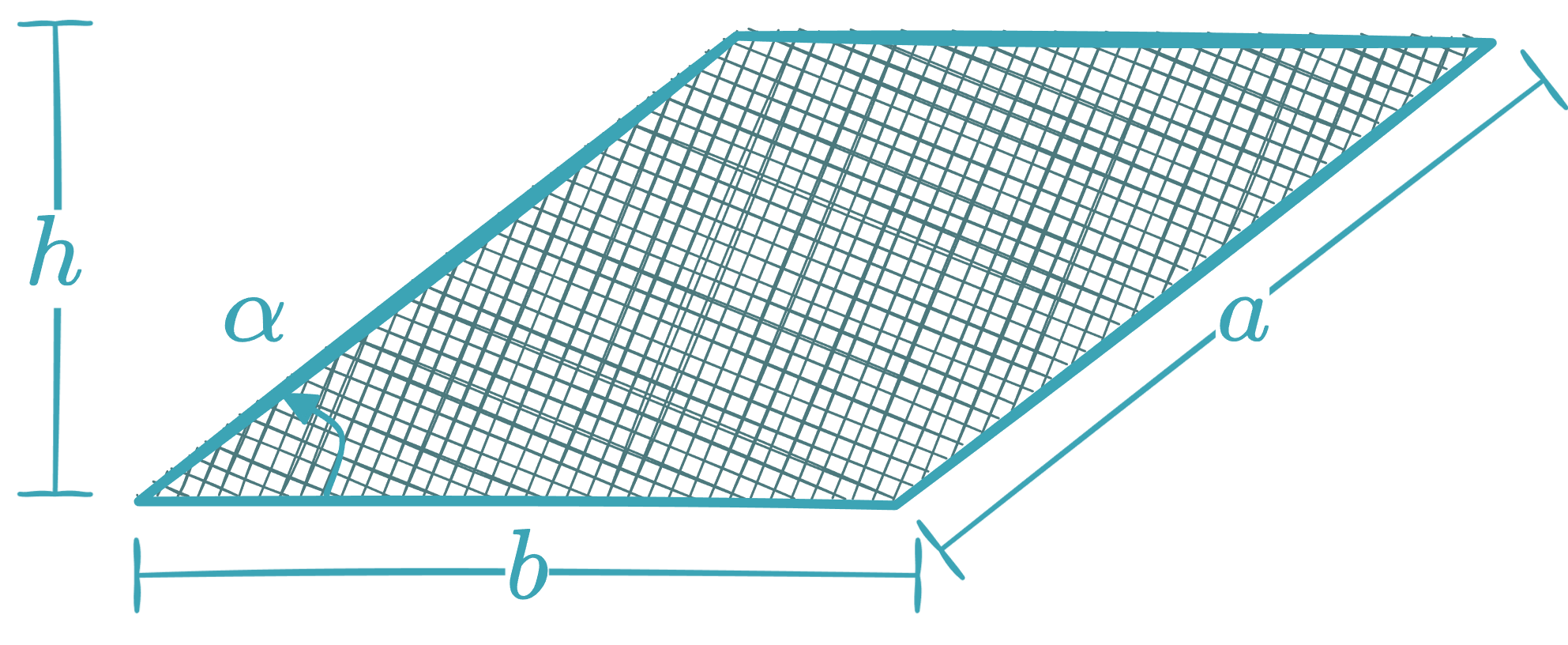
  $$A = b \cdot h = a \cdot b \cdot \sin \alpha$$

• Diagonals:

  $$d_1 = \sqrt{(a + h \cot \alpha)^2 + h^2}$$

  $$d_2 = \sqrt{(a - h \cot \alpha)^2 + h^2}$$

Trapezoid / Trapezium

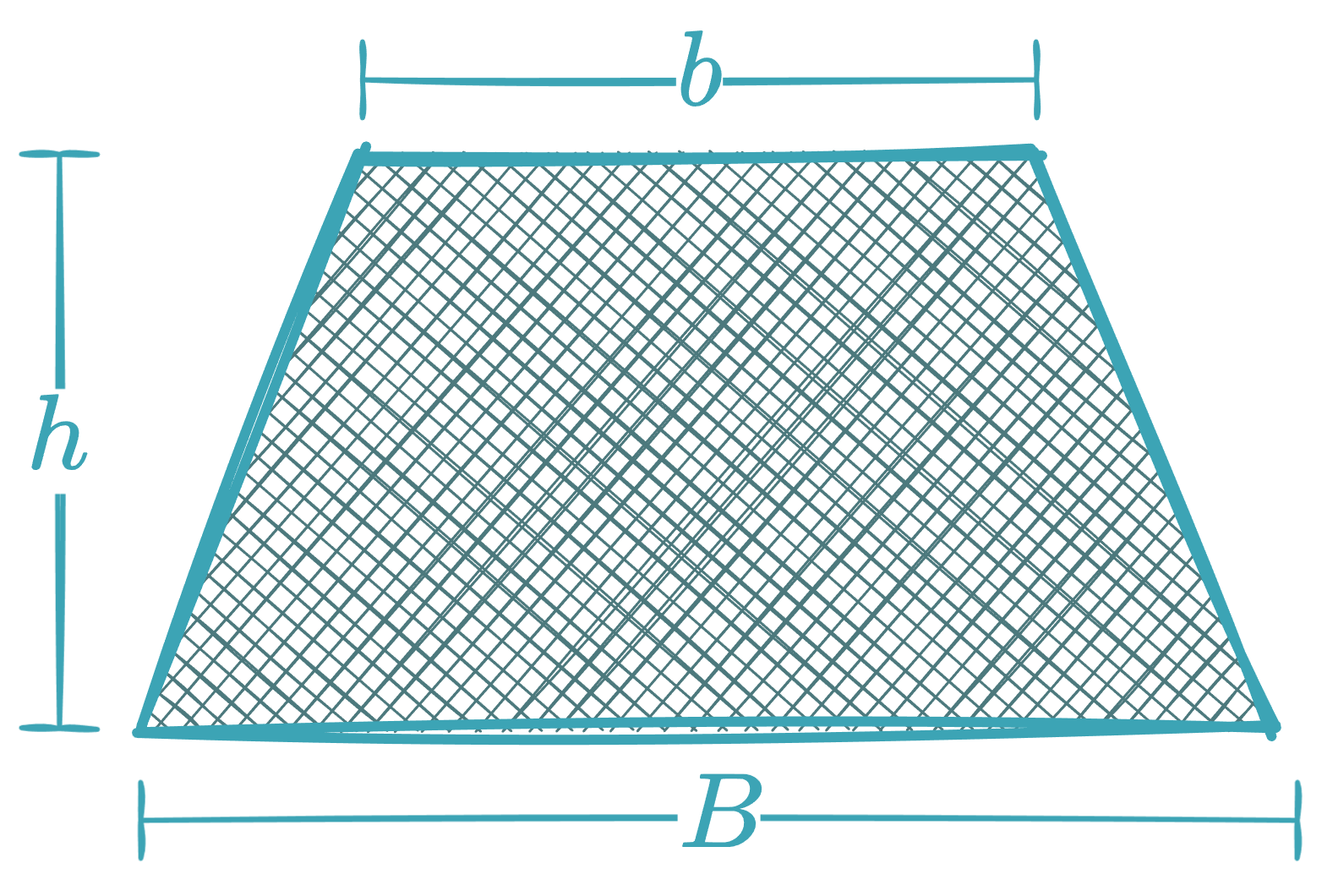
• Area:

  $$A = \frac{(B + b)}{2} \cdot h = m \cdot h$$

  (where $B$ and $b$ are the bases, $h$ the height and $m$ the midline)

• Midline:

  $$m = \frac{B + b}{2}$$

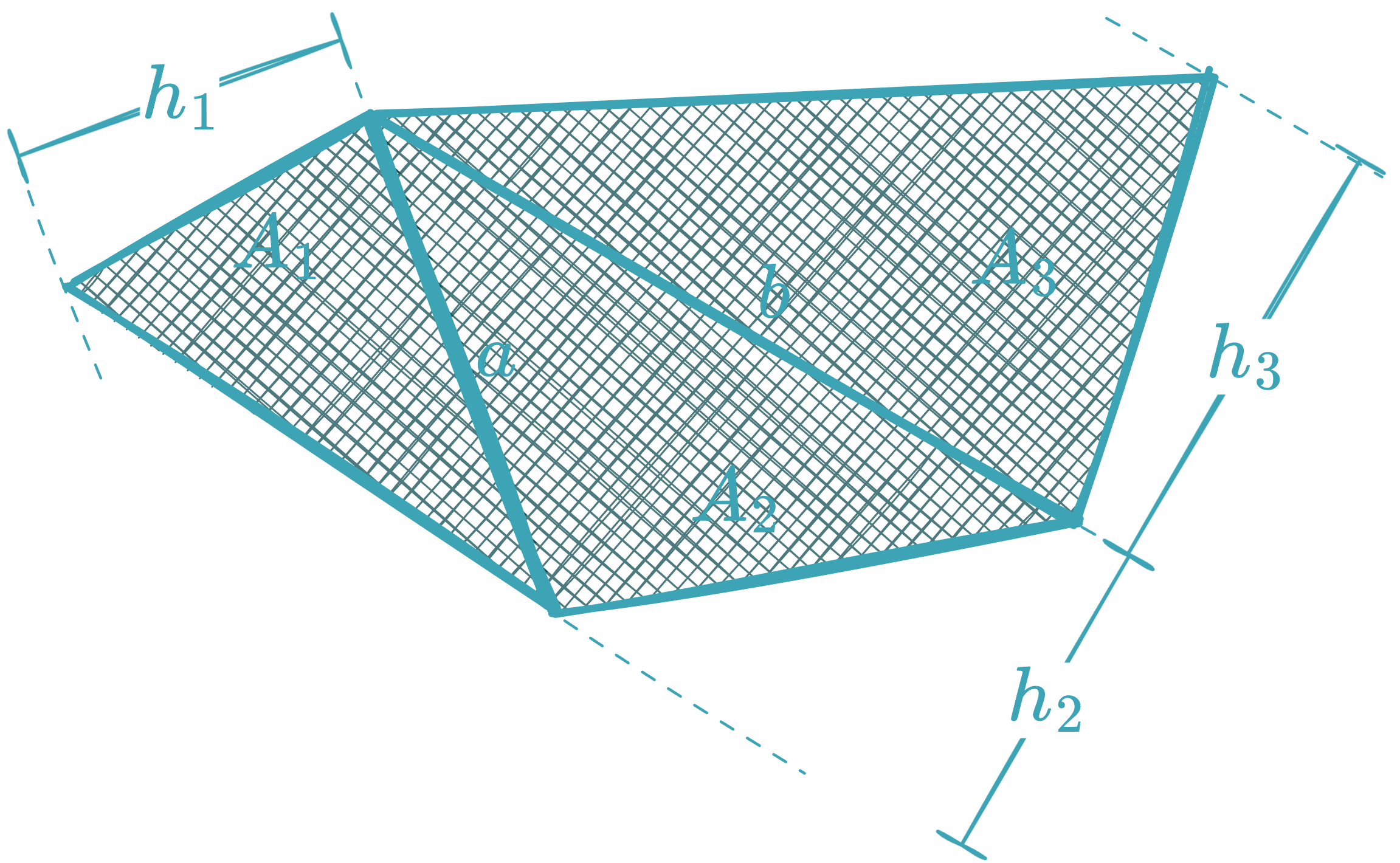
Trapezium / Irregular Quadrilateral

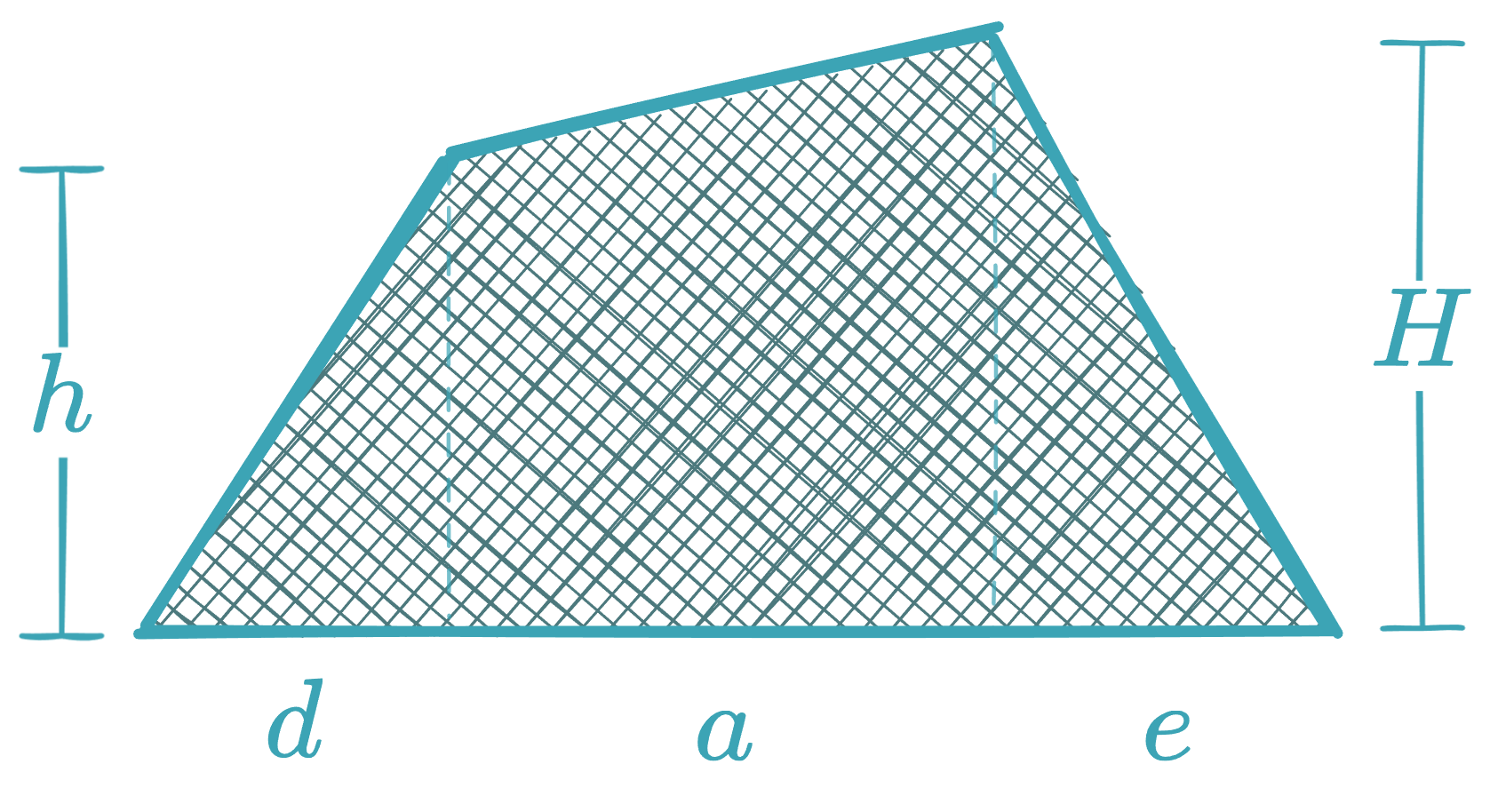
Can be calculated by dividing it into triangles:

$$A = \frac{a(H+h)+d \cdot h + e \cdot H}{2}$$

Regular Pentagon

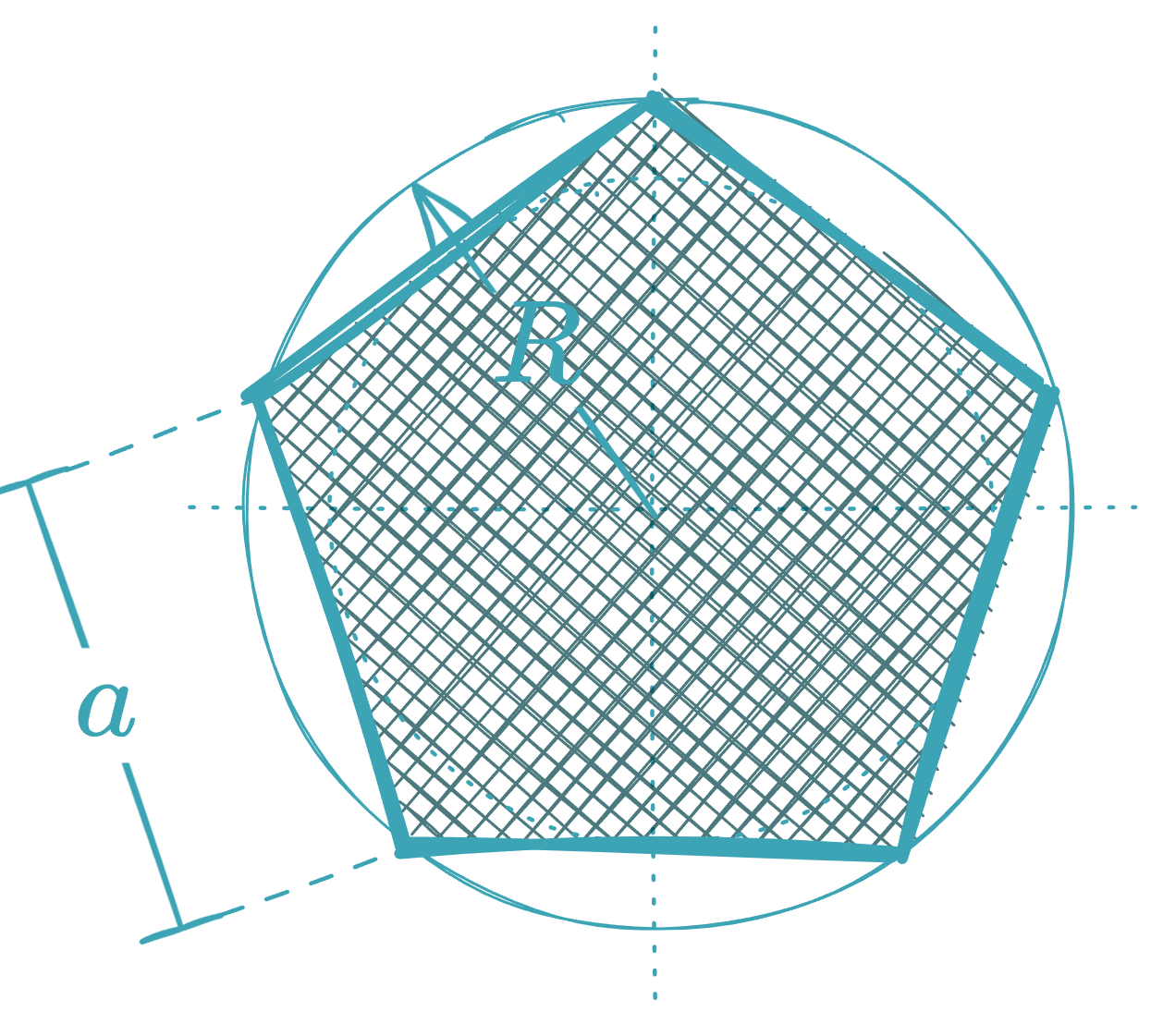
• In terms of the radius $R$ of the circumscribed circle:

  $$A = \frac{5}{8} R^2 \cdot \sqrt{10 + 2\sqrt{5}}$$

  $$A = \frac{5}{2}R^2 \cdot \sin 72^\circ$$

• In terms of side $a$:

  $$A = \frac{1}{4} \sqrt{5(5+2\sqrt{5})} \cdot a^2$$

• In terms of the apothem $a_{p}$:

  $$A = 5a_{p}^2 \cdot \sqrt{5 - 2\sqrt{5}}$$

  where the apothem is:

  $$a_{p}= \frac{a}{2} \cdot \sqrt{1 + \frac{2}{\sqrt{5}}}$$

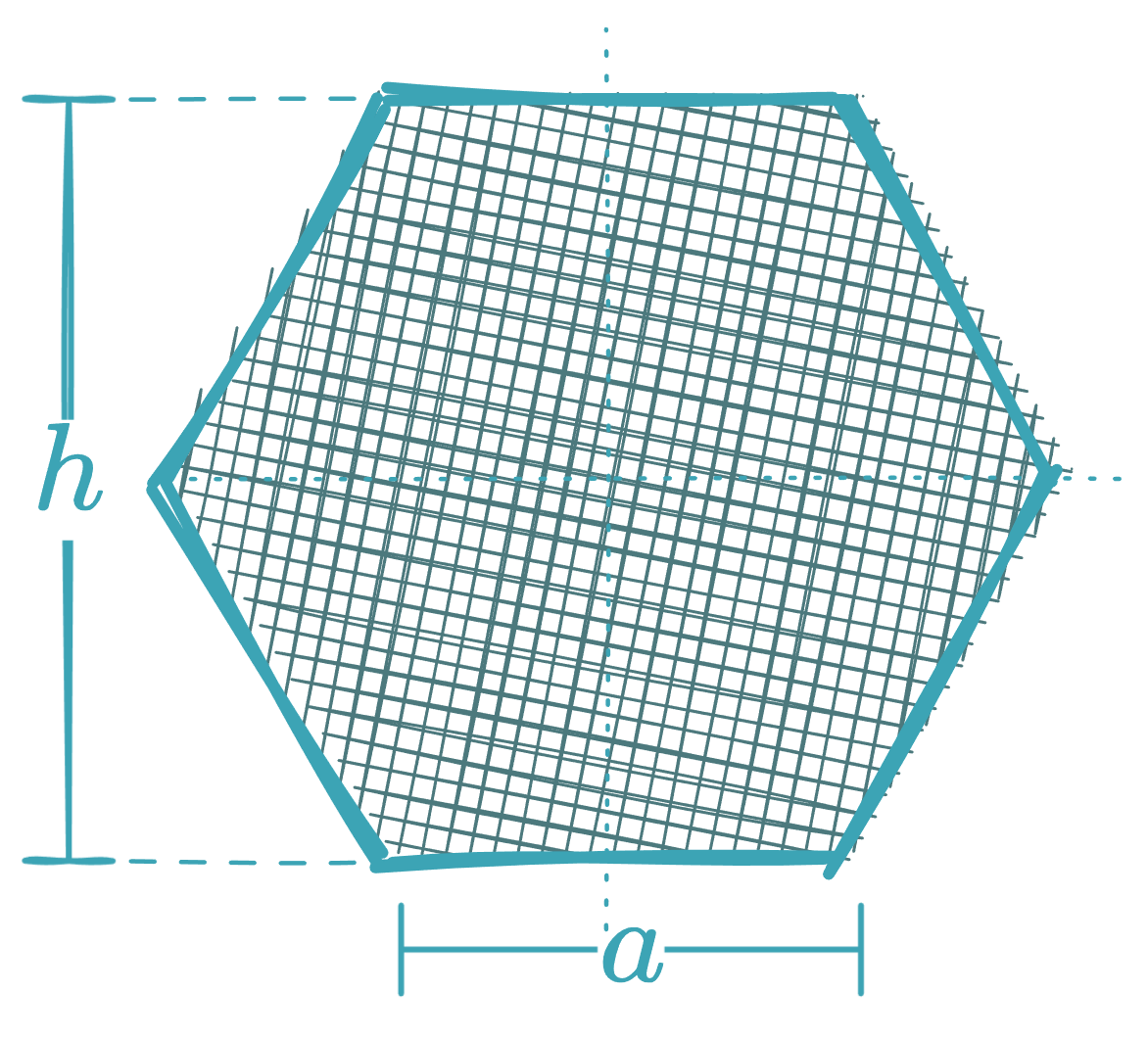
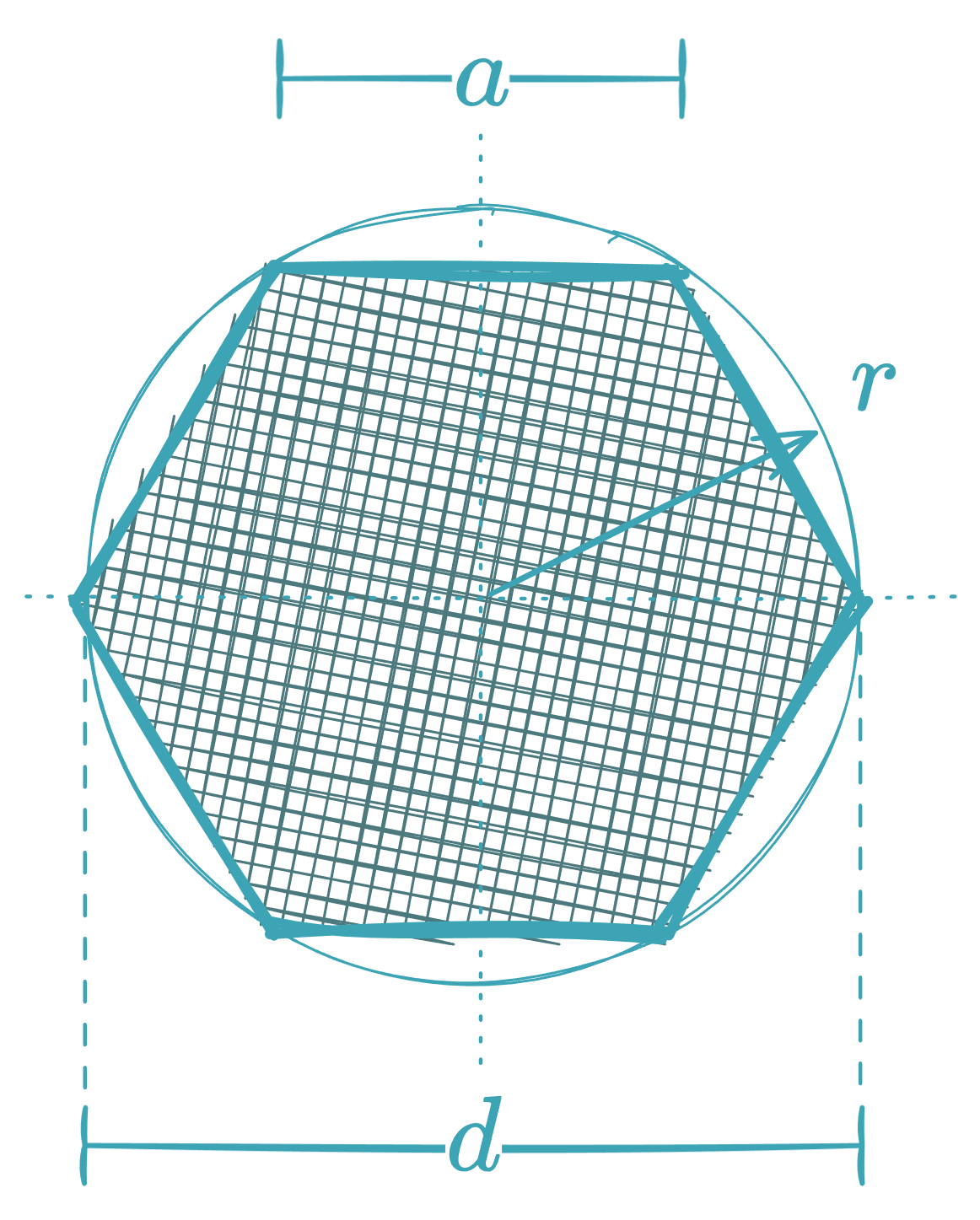
Regular Hexagon

• In terms of side $a$:

  $$A = \frac{3\sqrt{3}}{2} a^2$$

• In terms of the height between parallel sides $h$:

  $$A = \frac{\sqrt{3}}{2} h^2$$

• In terms of the major diagonal $d$:

  $$A = \frac{3\sqrt{3}}{4} d^2$$

• Important relations:
  The side $a$ is equal to the radius $R$ of the circumscribed circle: $a = R$.
  The height between parallel sides is: $h = \sqrt{3} \cdot a$.
  The major diagonal is: $d = 2a$.

Regular Octagon

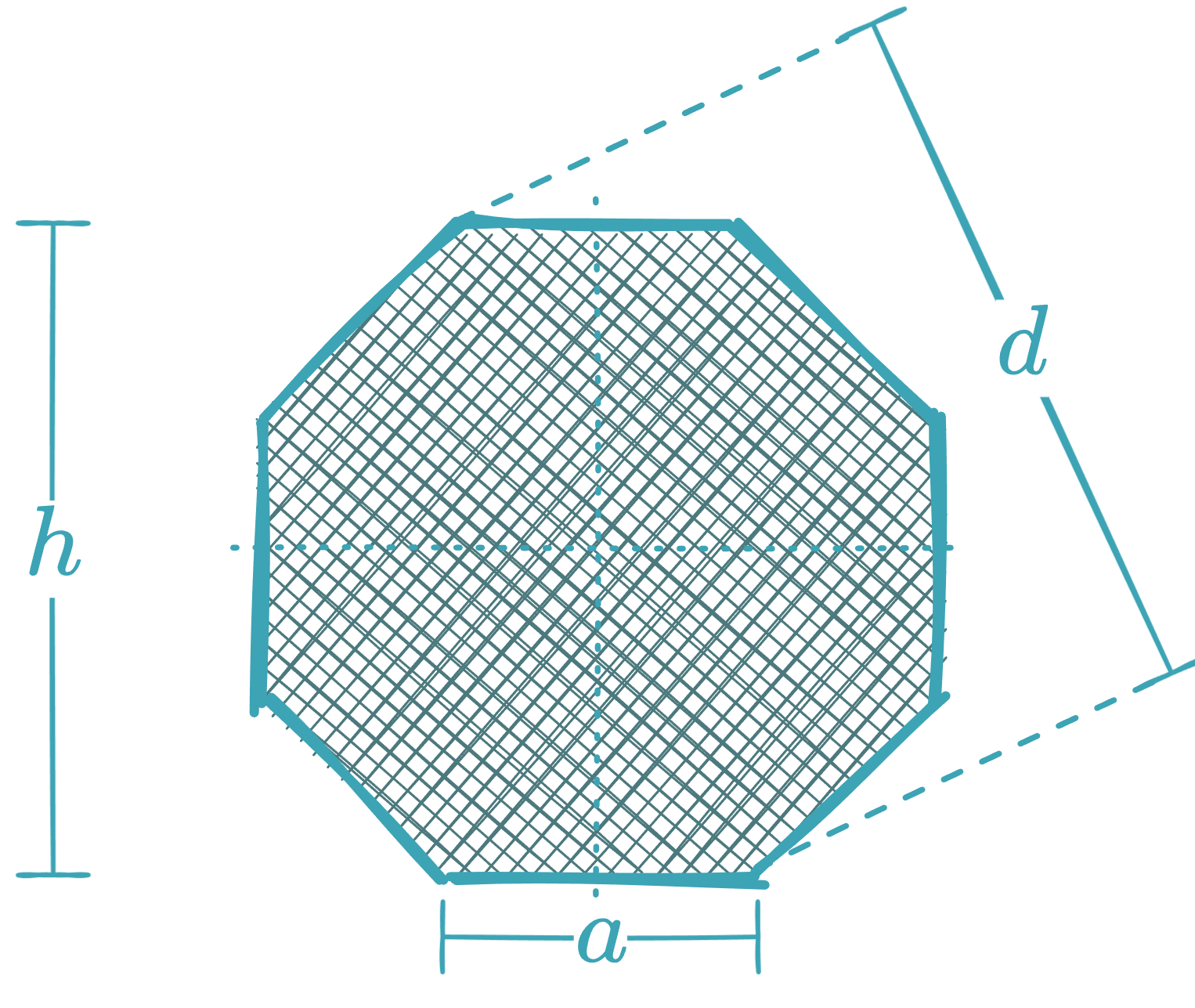
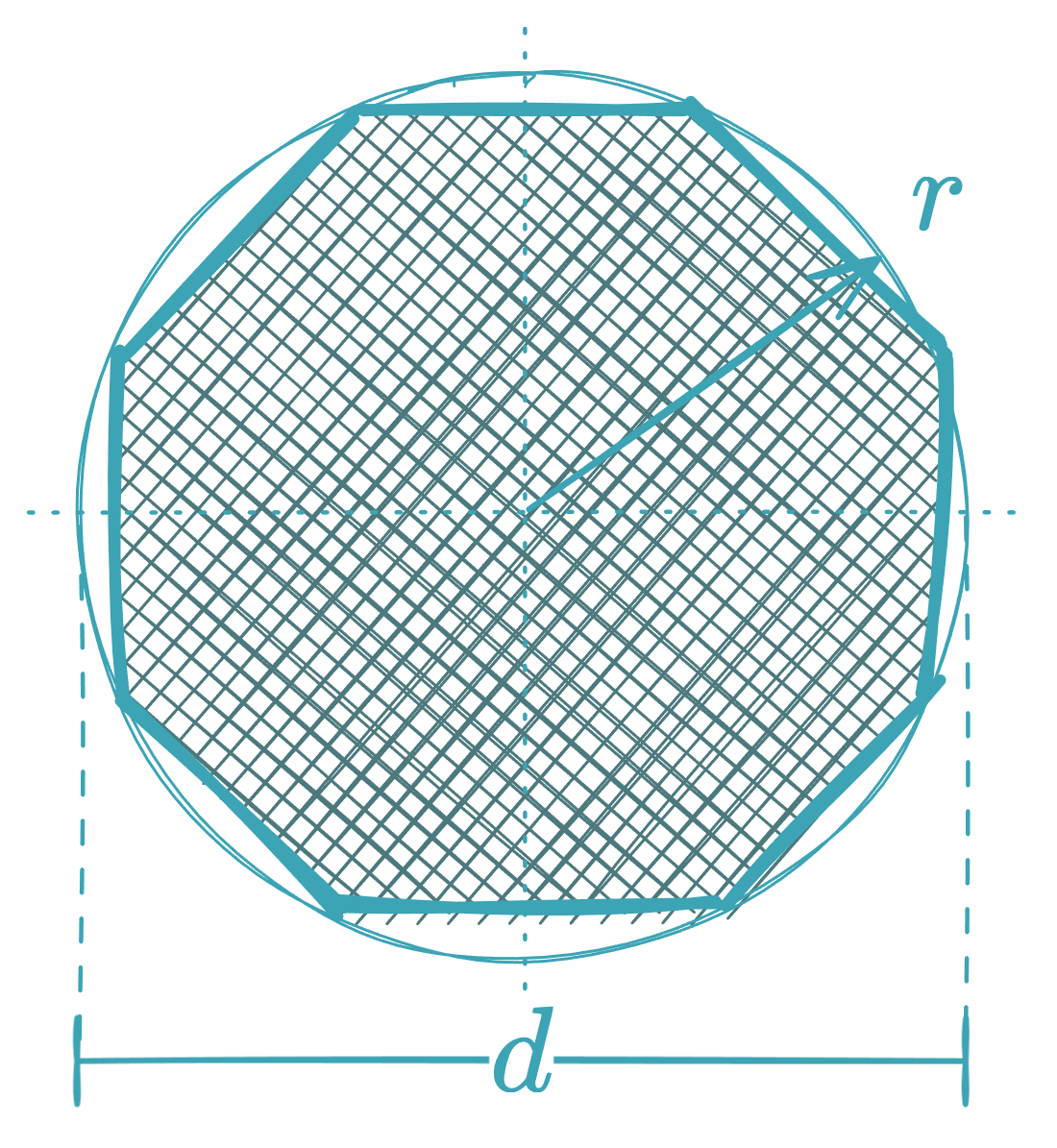
• Area in terms of side $a$ and apothem $a_{p}$:

  $$A = \frac{P \cdot a_{p}}{2} = 4 \cdot a \cdot a_{p}$$

• Perimeter:

  $$P = 8a$$

• Apothem:

  $$a_{p} = \frac{a}{2} \cdot \cot \frac{\pi}{8}$$

• Common approximate formulas:

  $$A = \frac{8a^2}{4\tan \frac{\pi}{8}} \approx 4.828 \cdot a^2$$

  $$A \approx 0.828 \cdot s^2$$

  (where $s$ is the width between parallel sides)

Irregular Polygon

Decomposed into triangles and their areas summed:

$$A_{\text{total}} = A_1 + A_2 + A_3 + \dots$$

$$A_{\text{total}} = \frac{a h_1 + b h_2 + b h_3 \dots}{2}$$

---

Area of the Circle and Sections of the Circle

Circle

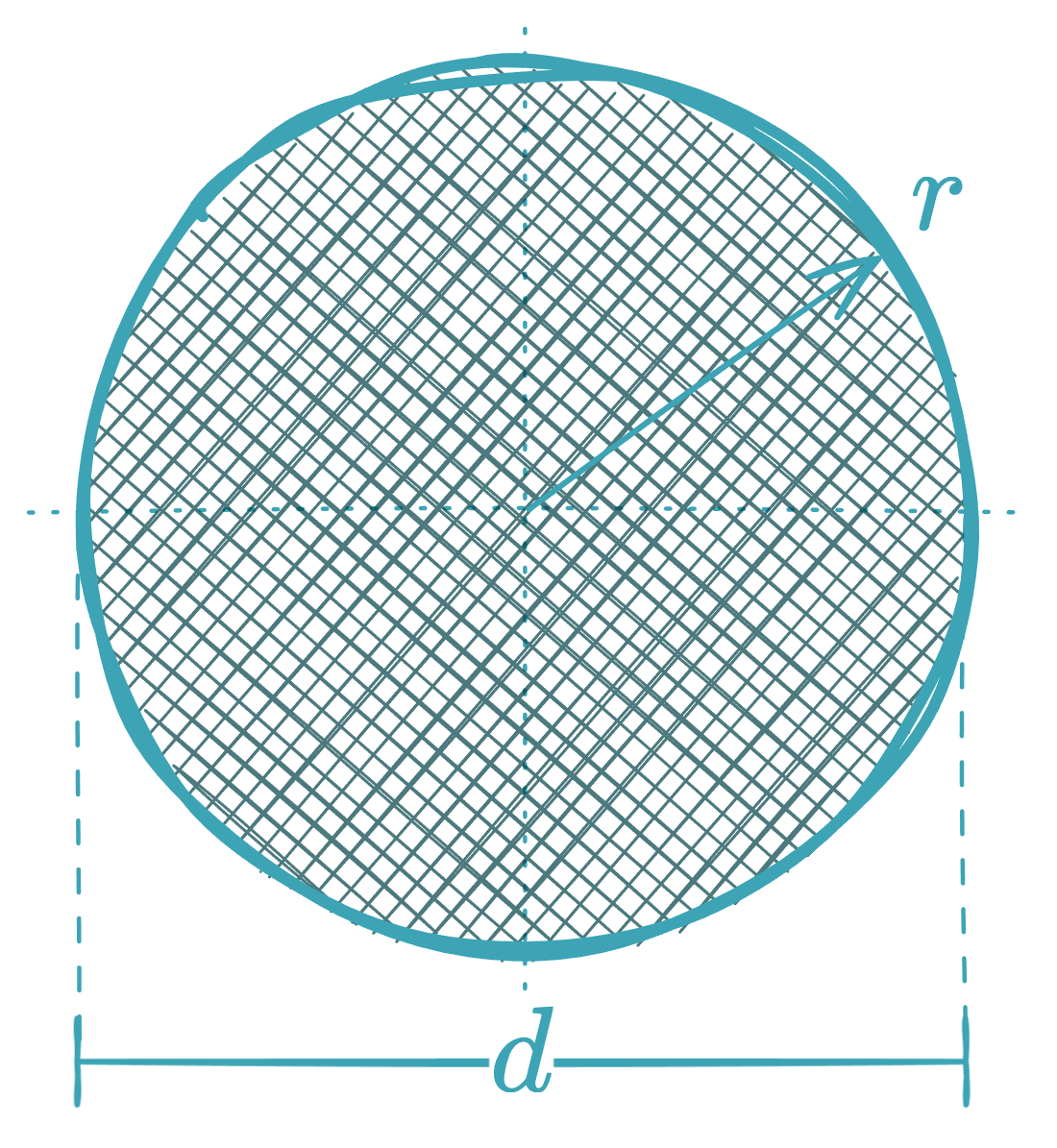
• Area in terms of diameter $d$:

  $$A = \frac{\pi}{4} d^2$$

• Area in terms of radius $r$:

  $$A = \pi r^2$$

Quadrant and Concave Triangle

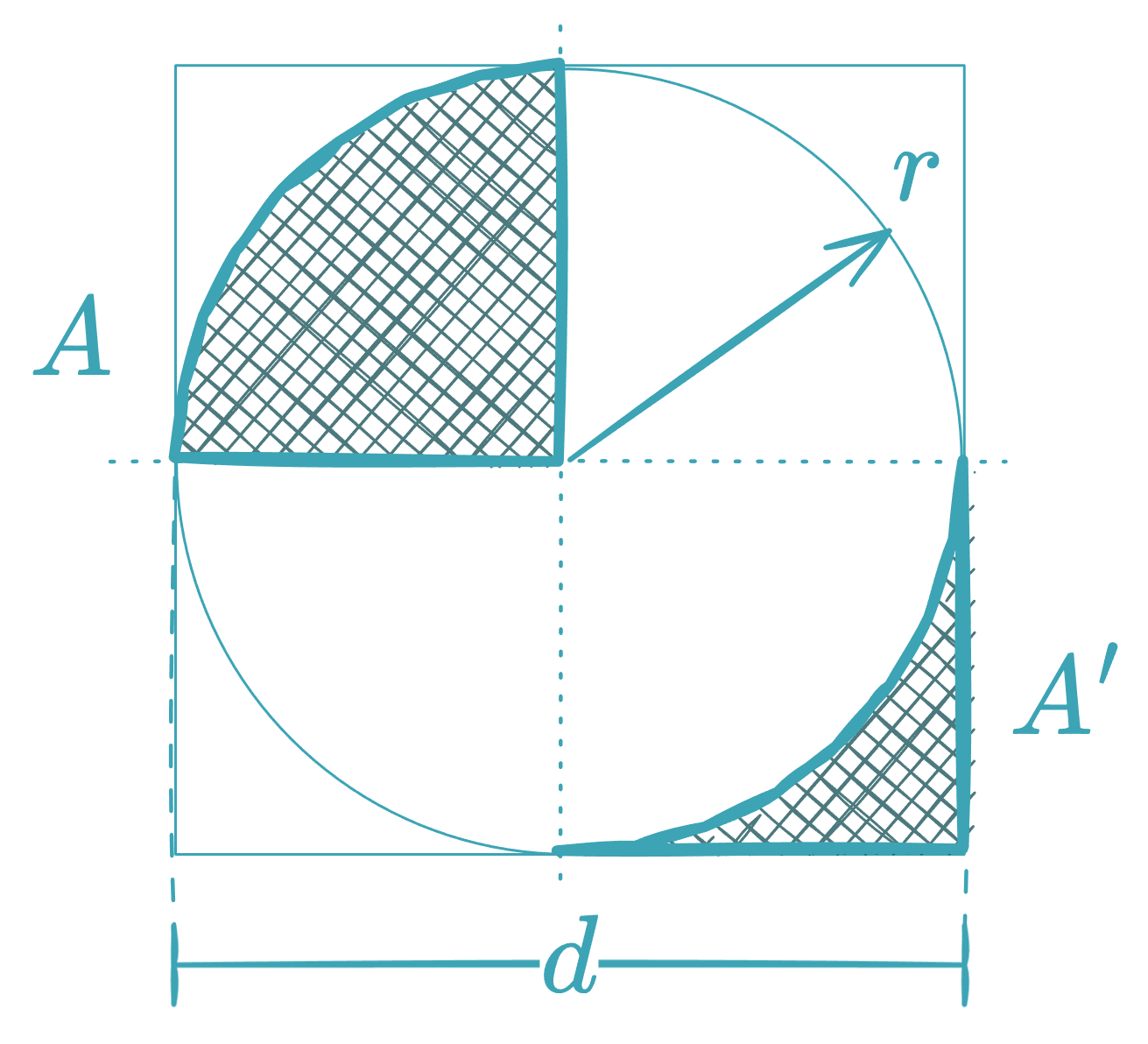
• Area of the quadrant:

  $$A = \frac{\pi}{16} d^2$$

  $$A = \frac{\pi}{4} r^2$$

• Area of the concave triangle:

  $$A' = \left(1 - \frac{\pi}{4}\right) r^2$$

(where $r$ is the radius and $d$ the diameter)

Circular Sector

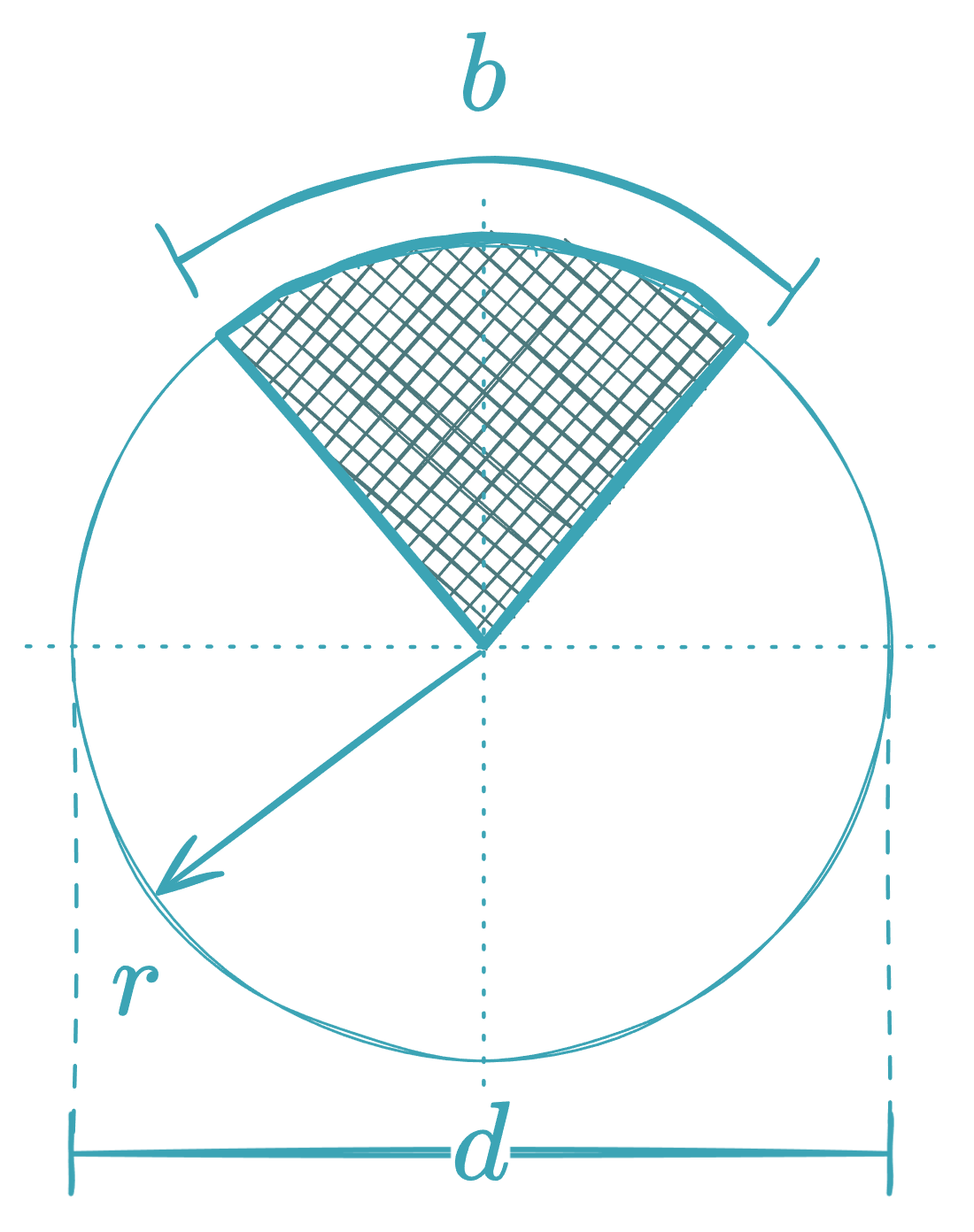
• Area (angle in degrees $\alpha^\circ$):

  $$A = \frac{\pi r^2 \alpha^\circ}{360^\circ}$$

• Area (angle in radians $\theta$):

  $$A = \frac{\theta}{2} r^2$$

• Arc length $L$:

  $$L = \frac{\pi r \alpha^\circ}{180^\circ} = \theta \cdot r$$

Circular Segment

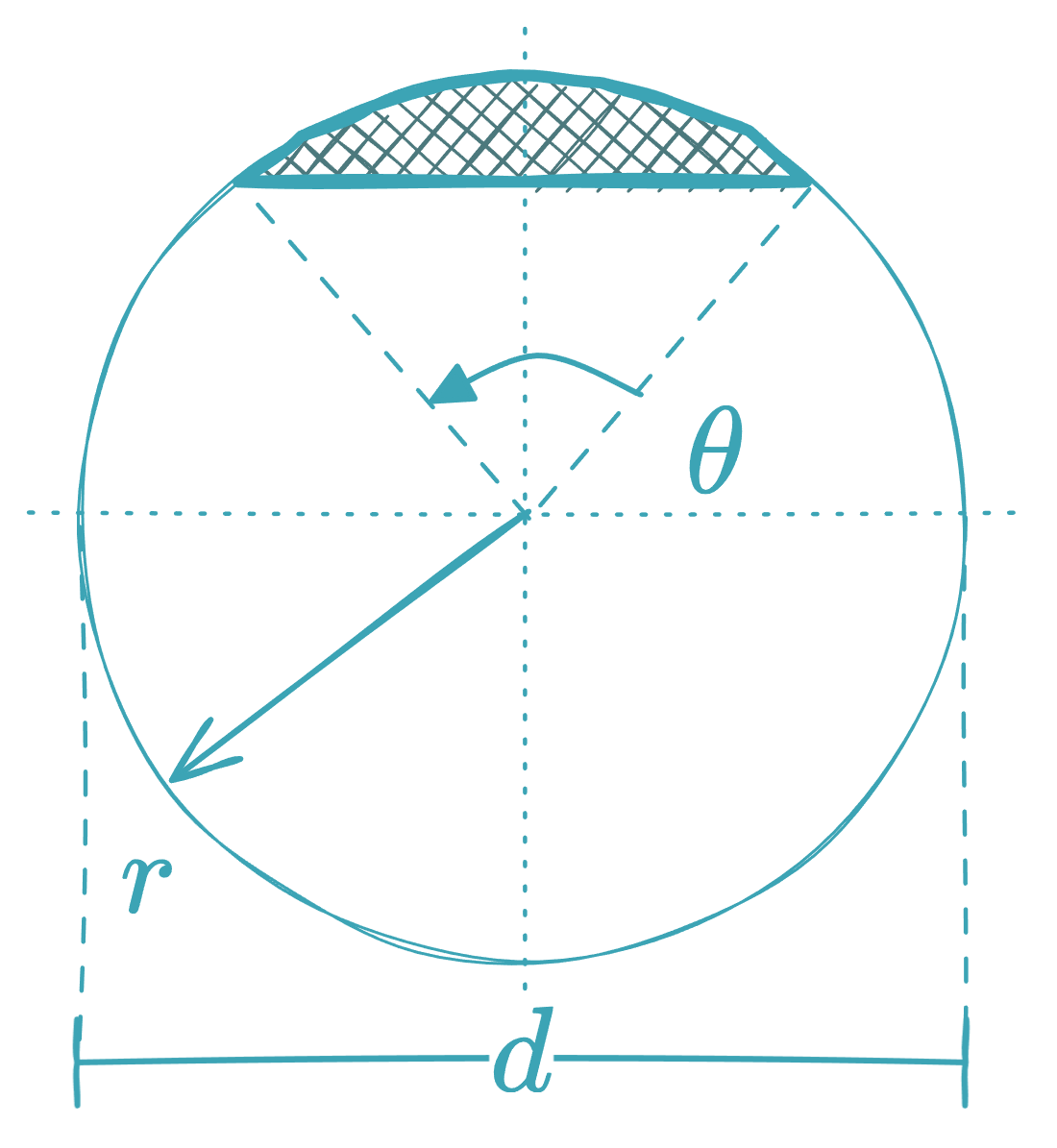
It is the area between a chord and its arc. Calculated by subtracting the area of the isosceles triangle formed by the radii and the chord from the area of the sector.

$$A = \frac{r^2}{2} (\theta - \sin \theta)$$

(where $\theta$ is in radians)

Annulus (Circular Ring)

• Area in terms of diameter:

  $$A = \frac{\pi}{4} (D^2 - d^2)$$

• Area in terms of radius:

  $$A = \pi (R^2 - r^2)$$

(where $R$ and $r$ are the radii, $D$ and $d$ the diameters)

Annular Sector (Circular Trapezoid)

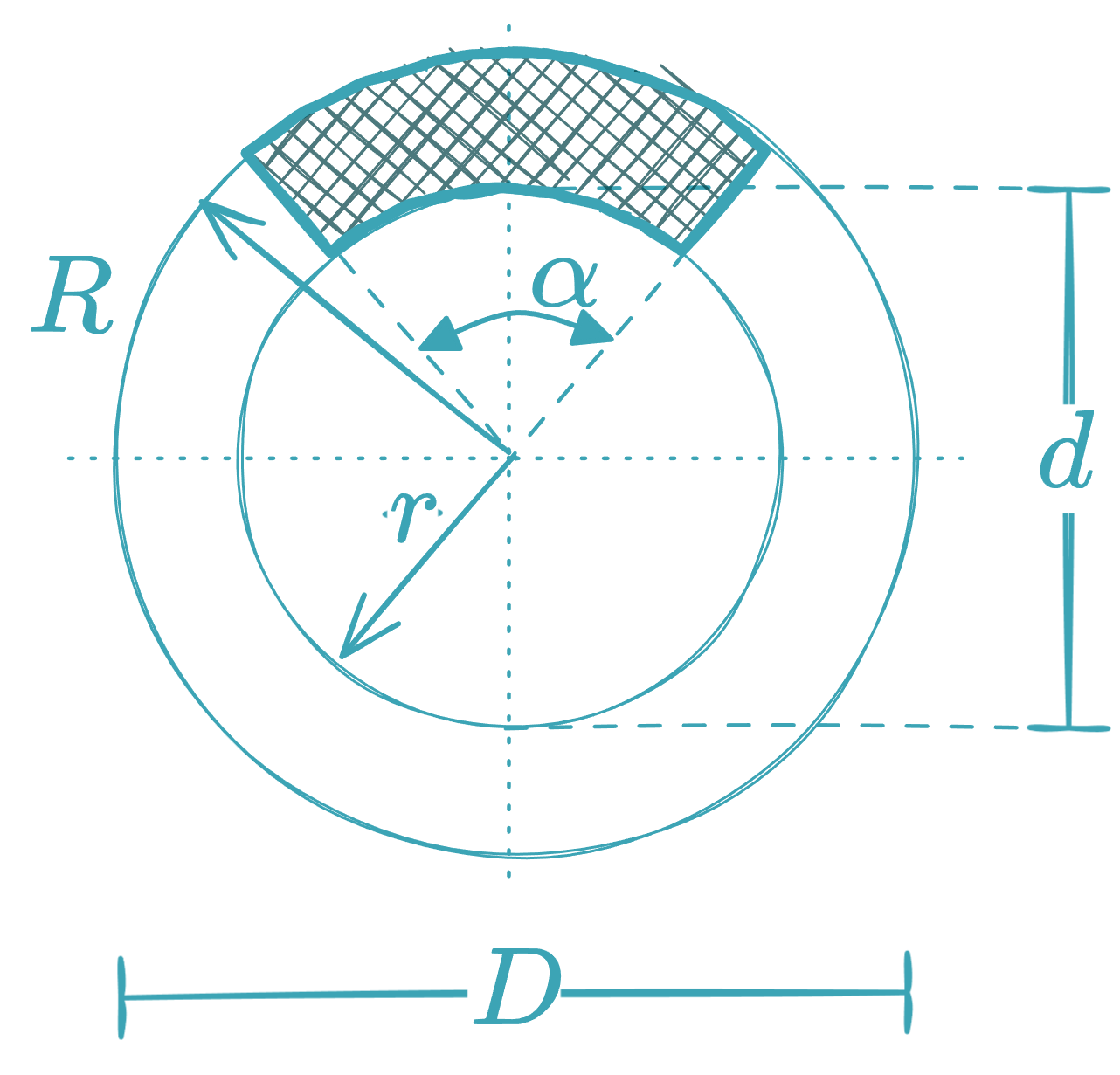
• Area (angle in degrees $\alpha^\circ$):

  $$A = \frac{\pi \cdot \alpha^\circ}{4 \cdot 360^\circ} (D^2 - d^2)$$

  $$A = \frac{\pi \alpha^\circ}{360^\circ} (R^2 - r^2)$$

• Area (angle in radians $\theta$):

  $$A = \frac{\theta}{8} (D^2 - d^2)$$

  $$A = \frac{\theta}{2} (R^2 - r^2)$$