Density

Absolute Density (ρ)

Absolute density is an intensive property that measures the concentration of mass per unit volume of a substance.

Fundamental Formula

$$\boxed{\rho = \frac{m}{V}}$$

where:

• $\rho$: Absolute density [kg/m³ (SI)]
• $m$: Mass of the substance [g, kg]
• $V$: Volume occupied [cm³, m³, L]

Common Units by State of Matter

• Solids and liquids: g/cm³, g/mL, kg/L, lb/ft³
• Gases: g/L, kg/m³ (at standard conditions)

Useful Conversion Factors

$$1 \text{ g/cm}^3 = 1000 \text{ kg/m}^3 = 1 \text{ kg/L}$$

$$1 \text{ lb/ft}^3 = 16.0185 \text{ kg/m}^3$$

Density of Some Substances at One Atmosphere of Pressure and 20°C

Densities measured at standard conditions (P = 1 atmosphere and T = 0°C)

Solids

Substance	S.I. (kg/m³)	Common (g/cm³)
Cork	240	0.24
Wood	500	0.50
Paper	700	0.70
NaCl	2160	2.16
Cu	8920	8.92
Au	19300	19.3
Os	22400	22.4
Lead	11300	11.3
Glass	2600	2.6
Brick (average)	1900	1.9
Hard Rubber	1200	1.2

Liquids

Substance	S.I. (kg/m³)	Common (g/cm³)
Chloroform	1500	1.50
Ethyl Alcohol	780	0.78
Oil	800	0.80
Seawater	1040	1.04
Milk	1030	1.03
Blood	1060	1.06
Bromine	3120	3.12
Mercury	13600	13.6
Glycerin	1260	1.26
Sulfuric Acid	1840	1.84
Gasoline (approx.)	670	0.67

Gases

Substance	S.I. (kg/m³)	Common (g/L)
H₂	0.09	0.09
Air	1.29	1.29
O₂	1.43	1.43
CO₂	1.98	1.98

---

Density of Mixtures (ρₘ)

For homogeneous or heterogeneous mixtures, the density is calculated as:

General Formula

$$\boxed{\rho_M = \frac{m_{\text{total}}}{V_{\text{total}}} = \frac{m_A + m_B + m_C + \cdots}{V_A + V_B + V_C + \cdots}}$$

Special Cases

1. Components with Equal Volumes

When each component occupies the same volume:

$$\rho_M = \frac{\rho_1 + \rho_2 + \cdots + \rho_n}{n}$$

Example: Mixture of 3 liquids with equal volumes:

$$\rho_M = \frac{\rho_1 + \rho_2 + \rho_3}{3}$$

2. Components with Equal Masses

When each component has the same mass:

$$\rho_M = \frac{n}{\frac{1}{\rho_1} + \frac{1}{\rho_2} + \cdots + \frac{1}{\rho_n}}$$

Example: Mixture of 2 substances with equal masses:

$$\rho_M = \frac{2}{\frac{1}{\rho_1} + \frac{1}{\rho_2}} = \frac{2\rho_1\rho_2}{\rho_1 + \rho_2}$$

---

Relative Density (Specific Gravity)

Relative density (ρᵣ or SG) is a dimensionless quantity that compares the density of a substance to a standard reference.

Formula

$$\boxed{\rho_r = SG = \frac{\rho_{\text{substance}}}{\rho_{\text{reference}}}}$$

Reference Substances

State	Reference Substance	Conditions	Reference Density
Solids and liquids	Pure water	4°C and 1 atm	$1.000 \text{ g/cm}^3$
Gases	Dry air	S.T.P. (0°C, 1 atm)	$1.2929 \text{ g/L}$

Interpretation

• SG < 1: The substance is less dense than the reference (floats)
• SG = 1: Density equal to the reference
• SG > 1: The substance is denser than the reference (sinks)

---

Specific Weight (γ)

An intensive property that relates the weight of a substance to its volume.

Definition and Formula

$$\boxed{\gamma = \frac{W}{V} = \frac{mg}{V} = \rho g}$$

Units

• International System (SI): N/m³
• Technical System: kgf/m³

Relationship with Density

$$\gamma = \rho \times g$$

Where $g = 9.80665 \text{ m/s}^2$ (standard acceleration of gravity)

---

Relative Specific Weight (γᵣ)

Relationship between the specific weight of a substance and that of the reference substance.

Important Property

$$\boxed{\gamma_r = \rho_r = SG}$$

Proof:

$$\gamma_r = \frac{\gamma_{\text{subst}}}{\gamma_{\text{ref}}} = \frac{\rho_{\text{subst}} g}{\rho_{\text{ref}} g} = \frac{\rho_{\text{subst}}}{\rho_{\text{ref}}} = \rho_r$$

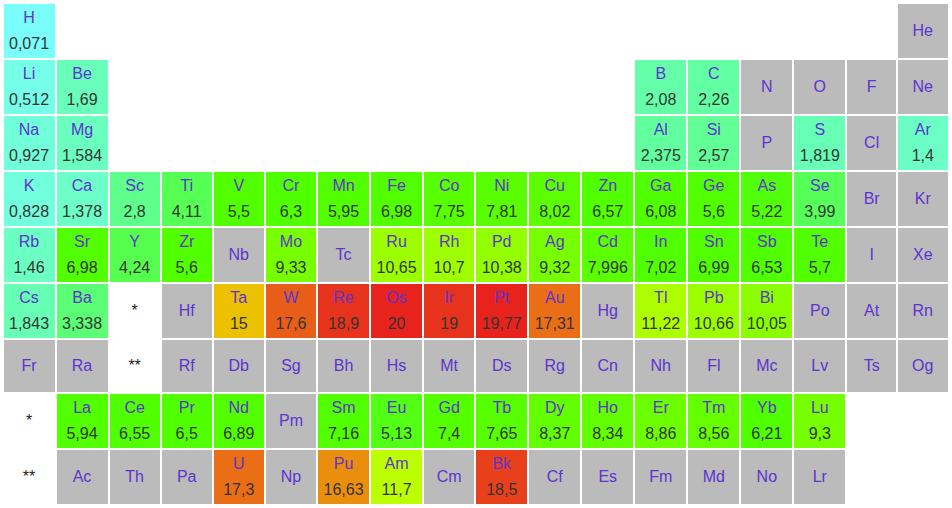
Density of Chemical Elements

Density of chemical elements under laboratory conditions, expressed in $\frac{g}{cm^3}$ (elements with a density greater than osmium or iridium only have a theoretical density: superheavy radioactive elements are produced in quantities too low or decay too rapidly to allow measurement):

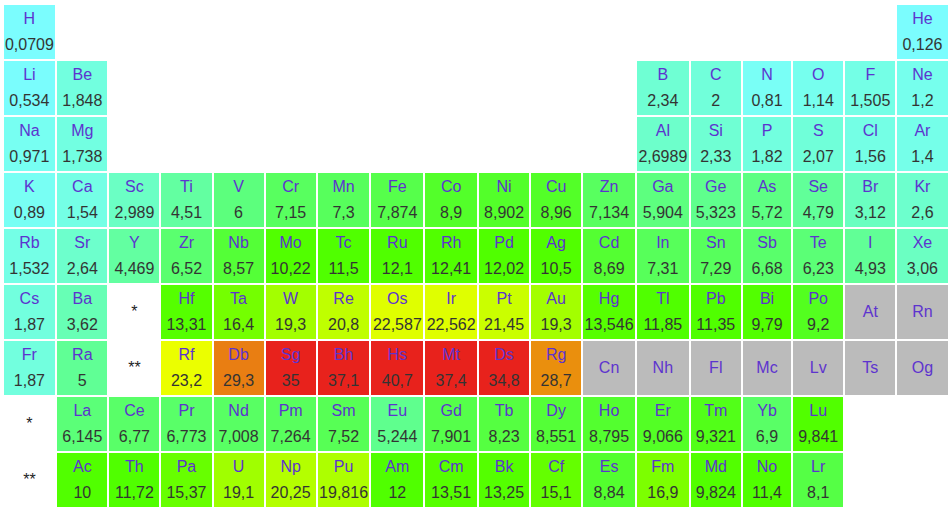
Density of the elements at their melting point in $\frac{g}{cm^3}$: